頂点データ管理

頂点データの適切なレイアウトと圧縮は、アプリが 2D のユーザー インターフェースで構成されている場合でも、3D のオープン ワールドゲームである場合でも、グラフィカル アプリのパフォーマンスにとって非常に重要です。Android GPU Inspector の Frame Profiler を使用していくつかの人気の Android ゲームの内部テストを行った結果、頂点データ管理には多くの改善の余地があることが判明しました。頂点データでは、フル精度、すべての頂点属性における 32 ビット浮動小数点数値、および完全にインターリーブされた属性でフォーマットされた構造の配列を使用する頂点バッファ レイアウトが一般的に使われていることがわかっています。

この記事では、以下の手法を使用して Android アプリのグラフィック パフォーマンスを最適化する方法について説明します。

• 頂点圧縮
• 頂点ストリーム分割

これらの手法を実装すると、頂点のメモリ帯域幅の使用率を最大で 50% 改善し、メモリバスの CPU との競合を軽減し、システムメモリのストールを削減し、バッテリー寿命を改善できます。これらはすべて、デベロッパーとエンドユーザーの双方にとってメリットになります。

ここで提示するすべてのデータは、Pixel 4 で実行される最大 19,000,000 個の頂点を含む静的シーンのサンプルに基づいています。

図 1: 6 個のリングと 1,900 万頂点を持つサンプルシーン

頂点圧縮

頂点圧縮は、効率的なパッキングを使用して実行時とストレージ内の両方で頂点データのサイズを削減する不可逆圧縮手法を指す包括的な用語です。頂点のサイズを縮小することには、いくつかのメリットがあります。たとえば、GPU のメモリ帯域幅の削減（帯域幅とコンピューティングのトレードオフによる）、キャッシュ利用率の改善、レジスタスピルのリスクの軽減などです。

頂点圧縮の一般的なアプローチは次のとおりです。

• 頂点データ属性の数値精度を下げる（例: 32 ビット浮動小数点数を 16 ビット浮動小数点数に変換する）
• さまざまな形式で属性を表現する

たとえば、頂点が位置座標（vec3）、標準座標（vec3）、テクスチャ座標（vec2）でフル 32 ビット浮動小数点数を使用している場合、それらをすべて 16 ビット浮動小数点数に置き換えると、頂点サイズが 50%（平均的な 32 バイトの頂点では 16 バイト）削減されます。

頂点位置

頂点位置データは、大部分のメッシュで、フル精度 32 ビット浮動小数点数値から半精度 16 ビット浮動小数点数値に圧縮できます。半精度浮動小数点数は、ほとんどすべてのモバイル デバイスのハードウェアでサポートされています。float32 を float16 に変換する関数は次のようになります（こちらのガイドの例を加工したものです）。

uint16_t f32_to_f16(float f) {
  uint32_t x = (uint32_t)f;
  uint32_t sign = (unsigned short)(x >> 31);
  uint32_t mantissa;
  uint32_t exp;
  uint16_t hf;

  mantissa = x & ((1 << 23) - 1);
  exp = x & (0xFF << 23);
  if (exp >= 0x47800000) {
    // check if the original number is a NaN
    if (mantissa && (exp == (0xFF << 23))) {
      // single precision NaN
      mantissa = (1 << 23) - 1;
    } else {
      // half-float will be Inf
      mantissa = 0;
    }
    hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
         (uint16_t)(mantissa >> 13);
  }
  // check if exponent is <= -15
  else if (exp <= 0x38000000) {
    hf = 0;  // too small to be represented
  } else {
    hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
         (uint16_t)(mantissa >> 13);
  }

  return hf;
}

このアプローチには限界があります。つまり、頂点が起点から遠ざかるにつれて精度が低下し、非常に大きな空間を占めるメッシュ（1,024 を超える要素を持つ頂点）では適切に機能しなくなります。この問題を解決するには、メッシュを小さなチャンクに分割し、モデルの起点を中心にして各チャンクを配置します。さらに、各チャンクのすべての頂点が [-1, 1] の範囲（浮動小数点数値の最も高い精度を含む）に収まるようにスケーリングします。圧縮用の疑似コードは次のようになります。

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));

レンダリング時に頂点データを解凍するために、スケーリング ファクタと変換をモデル マトリックスにベイクします。この同じ圧縮マトリックスを標準座標の変換に使用しないでください。それらには同じ圧縮が適用されていないからです。標準座標には、これらの解凍変換を使用しないマトリックスが必要です。基本モデル マトリックス（標準座標に使用可能）を使用すると、シェーダー内のモデル マトリックスに追加の解凍変換を適用できます。次に例を示します。

vec3 in in_pos;

void main() {
   ...
   // bounding box data packed into uniform buffer
   vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
   gl_Position = proj * view * model * decompress_pos;
}

別のアプローチとしては、符号付き正規化整数（SNORM）を使用します。SNORM のデータ型は、浮動小数点数ではなく整数で [-1, 1] の範囲内の数値を表現します。位置座標に 16 ビット SNORM を使用すると、不均一分布のデメリットがない float16 と同様のメモリ節約が可能になります。SNORM を使用するおすすめの実装は次のようになります。

const int BITS = 16

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   // float to integer value conversion
   p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1) 

	形式	サイズ
変換前	vec4<float32>	16 バイト
変換後	vec3<float16/SNORM16>	6 バイト

頂点の標準座標とタンジェント空間

ライティングには頂点の標準座標が必要であり、標準マッピングのようなより複雑な手法にはタンジェント空間が必要です。

タンジェント空間

タンジェント空間とは、すべての頂点が標準ベクトル、タンジェント ベクトル、バイタンジェント ベクトルで構成される座標系です。通常、これら 3 つのベクトルは互いに直交しているため、そのうちの 2 つを格納するだけでよく、3 つ目のベクトルは頂点シェーダーで他の 2 つのクロス積を取ることにより計算できます。

一般的に、これらのベクトルは視覚的忠実度の損失なしに 16 ビット浮動小数点数で表現できるので、最初はこれらから始めるとよいでしょう。

タンジェント空間全体を単一の四元数に格納する QTangent という手法を使用すると、さらなる圧縮が可能です。四元数は回転を表現するために使用できるので、タンジェント空間ベクトルを回転（この場合はモデル空間からタンジェント空間への回転）を表す 3x3 マトリックスの列ベクトルと見なすことにより、この 2 つを相互に変換できます。四元数は vec4 に似たデータとして扱うことができます。タンジェント空間ベクトルの QTangent への変換は、次のようになります。これは上記のリンクにある論文に基いており、こちらの実装から加工されたものです。

const int BITS = 16

quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
   mat3 tbn = {normal, tangent, bitangent};
   quaternion qTangent(tbn);
   qTangent.normalize();

   //Make sure QTangent is always positive
   if (qTangent.w < 0)
       qTangent = -qTangent;

   const float bias = 1.0 / (2^(BITS - 1) - 1);

   //Because '-0' sign information is lost when using integers,
   //we need to apply a "bias"; while making sure the Quaternion
   //stays normalized.
   // ** Also our shaders assume qTangent.w is never 0. **
   if (qTangent.w < bias) {
       Real normFactor = Math::Sqrt( 1 - bias * bias );
       qTangent.w = bias;
       qTangent.x *= normFactor;
       qTangent.y *= normFactor;
       qTangent.z *= normFactor;
   }

   //If it's reflected, then make sure .w is negative.
   vec3 naturalBinormal = cross_product(tangent, normal);
   if (dot_product(naturalBinormal, binormal) <= 0)
       qTangent = -qTangent;
   return qTangent;
}

四元数は正規化され、SNORM を使用して圧縮できます。16 ビット SNORM では、高い精度とメモリ節約が可能になります。8 ビット SNORM を使用するとさらにメモリを節約できますが、鏡面反射性が高いマテリアルではアーティファクトが発生する可能性があります。両方を試して、どれがアセットに最適かを確認するとよいでしょう。四元数のエンコードは次のようになります。

for each vertex v in mesh:
   quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
   // Once we have the quaternion we can compress it
   res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);

頂点シェーダーの四元数をデコードするには、次のようなコードを使用します（こちらの例を加工したものです）。

vec3 xAxis( vec4 qQuat )
{
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwy = fTy * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxy = fTy * qQuat.x;
  float fTxz = fTz * qQuat.x;
  float fTyy = fTy * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}

vec3 yAxis( vec4 qQuat )
{
  float fTx  = 2.0 * qQuat.x;
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwx = fTx * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxx = fTx * qQuat.x;
  float fTxy = fTy * qQuat.x;
  float fTyz = fTz * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}

void main() {
  vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
  vec3 normal = xAxis(qtangent);
  vec3 tangent = yAxis(qtangent);
  float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
  vec3 binormal = cross(normal, tangent) * biNormalReflection;
  ...
}

	形式	サイズ
変換前	vec3<float32>+ vec3<float32>+ vec3<float32>	36 バイト
変換後	vec4<SNORM16>	8 バイト

標準座標のみ

標準ベクトルのみを格納すればよい場合は、別のアプローチを使ってさらにメモリを節約できます。それは、標準ベクトルを圧縮するためにデカルト座標ではなく単位ベクトルの八面体マッピングを使用する方法です。八面体マッピングでは、単位球を八面体に投影した後、八面体を 2D 平面に投影します。したがって、2 つの数値だけで標準ベクトルを表現できます。この 2 つの数値は、球を投影した 2D 平面を「サンプリング」して元のベクトルを回復するために使用できるテクスチャ座標と見なすことができます。この 2 つの数値は SNORM8 に格納できます。

図 2: 可視化された八面体マッピング（出典）

const int BITS = 8

// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
  float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
  vec2 res;
  if (n.z < 0.0) {
    res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
    res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
  } else {
    res.x = n.x * invL1Norm;
    res.y = n.y * invL1Norm;
  }
  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

頂点シェーダー内の解凍（デカルト座標に戻す変換）は低コストです。最新のモバイル デバイスでは、この手法を実装した場合にパフォーマンスの大幅な低下は見られませんでした。頂点シェーダー内の解凍は次のようになります。

//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
  vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
  float t = max(-v.z, 0.0);
  v.xy += t * -sign(v.xy);
  return v;

このアプローチを使ってタンジェント空間全体を格納することもできます。この手法では vec2<SNORM8> を使用して標準ベクトルとタンジェント ベクトルを格納しますが、バイタンジェントの向きを格納する方法を見つける必要があります（これは、モデルで UV 座標をミラーリングする一般的なシナリオで必要です）。これを実装するには、タンジェント ベクトルのエンコードのコンポーネントを常に正数にマッピングし、次にバイタンジェントの向きを逆にする必要がある場合は符号を逆転して、頂点シェーダーでそれをチェックする方法があります。

const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)

// Compressing
for each normal n in mesh:
  //encode to octahedron, result in range [-1, 1]
  vec2 res = vec_to_oct(n);

  // map y to always be positive
  res.y = res.y * 0.5 + 0.5;

  // add a bias so that y is never 0 (sign in the vertex shader)
  if (res.y < bias)
    res.y = bias;

  // Apply the sign of the binormal to y, which was computed elsewhere
  if (binormal_sign < 0)
    res.y *= -1;

  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);

	形式	サイズ
変換前	vec3<float32>	12 バイト
変換後	vec2<SNORM8>	2 バイト

頂点 UV 座標

UV 座標は、特にテクスチャ マッピングで使用される場合、通常は 32 ビット浮動小数点数で格納されます。16 ビット浮動小数点数で圧縮すると、1024x1024 より大きいテクスチャでは精度の問題が生じます。[0.5, 1.0] の範囲内の浮動小数点精度は、数値の増分が 1 ピクセルより大きいことを意味します。

より優れたアプローチは、符号なし正規化整数（UNORM）、特に UNORM16 を使用することです。そうすれば、テクスチャ座標範囲全体にわたって均一分布が提供され、最大 65536x65536 のテクスチャがサポートされます。ここでは、テクスチャ座標が要素ごとに [0.0, 1.0] の範囲内にあると仮定していますが、メッシュによってはこれに当てはまらない場合があります（たとえば、壁は 1.0 を超えるラッピング テクスチャ座標を使用する可能性があります）。したがって、この手法を検討する場合は、その点に留意してください。変換関数は次のようになります。

const int BITS = 16

for each vertex_uv V in mesh:
  V *= clamp(2^BITS - 1, 0, 2^BITS - 1);  // float to integer value conversion

	形式	サイズ
変換前	vec2<float32>	8 バイト
変換後	vec2<UNORM16>	4 バイト

頂点圧縮の結果

上記の頂点圧縮手法では、頂点メモリのストレージが 66% 削減され、48 バイトから 16 バイトになりました。この結果は次のように現れました。

• 頂点のメモリ読み取り帯域幅:
  • ビニング: 27 GB/秒から 9 GB/秒に
  • レンダリング: 4.5 GB/秒から 1.5 GB/秒に
• 頂点のフェッチ ストール:
  • ビニング: 50% から 0% に
  • レンダリング: 90% から 90% に
• 頂点ごとの平均バイト数:
  • ビニング: 48 バイトから 16 バイトに
  • レンダリング: 52 バイトから 18 バイトに

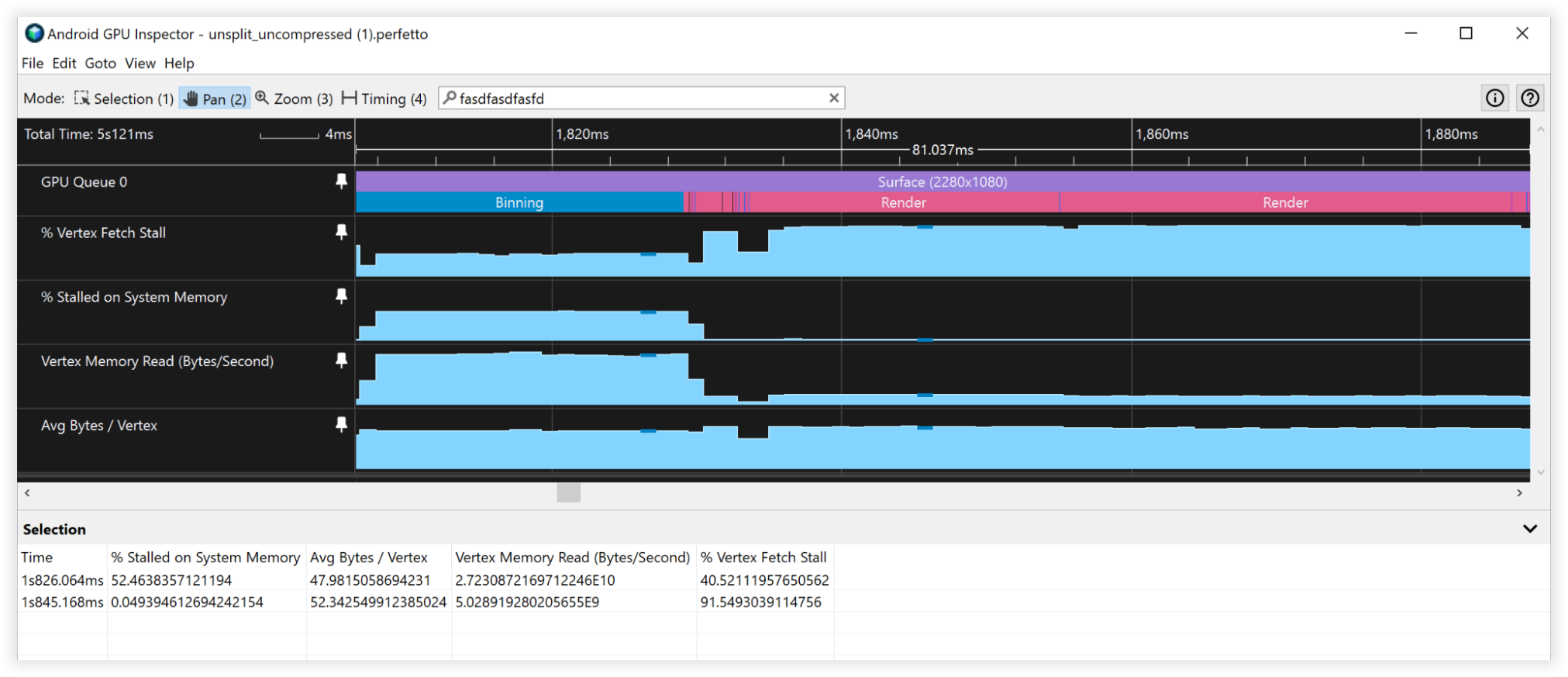
図 3: 非圧縮頂点の Android GPU Inspector ビュー

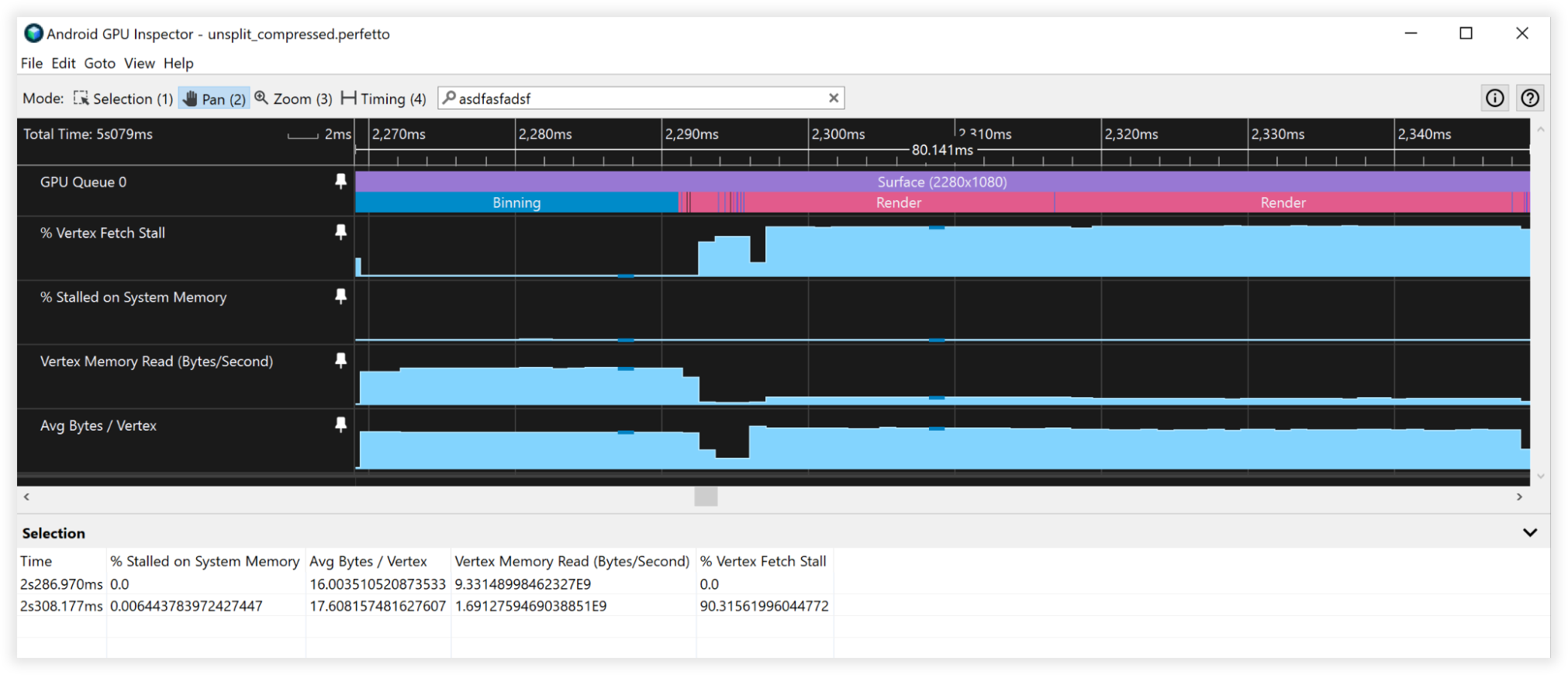
図 4: 圧縮された頂点の Android GPU Inspector ビュー

頂点ストリーム分割

頂点ストリーム分割は、頂点バッファ内のデータの構成を最適化します。これはキャッシュ パフォーマンスの最適化であり、Android デバイスでよく見られるタイルベースの GPU で効力を発揮します。特に、レンダリング プロセスのビニング ステップで効果的です。

タイルベースの GPU は、ビニングを行う指定された頂点シェーダーに基づいて、正規化されたデバイス座標を計算するシェーダーを作成します。これは、最初にシーン内のすべての頂点（表示されているかどうかを問わない）で実行されます。メモリ内で頂点位置データの連続性を維持することには、大きな利点があります。この頂点ストリーム レイアウトは、シャドウパスにもメリットをもたらします。通常、シャドウ計算に必要なのは、位置データに加えて、コンソール / デスクトップのレンダリングでよく使用される手法である深度プリパスのみであるからです。この頂点ストリーム レイアウトは、レンダリング エンジンの複数のクラスにとってもメリットとなる可能性があります。

ストリーム分割では、頂点位置データの連続したセクションと、インターリーブされた頂点属性を含む別のセクションで頂点バッファを設定します。通常、ほとんどのアプリは、すべての属性を完全にインターリーブするバッファを設定します。この違いを次に示します。

Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|

After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|

GPU が頂点データをフェッチする方法を検討することは、ストリーム分割の利点を理解するのに役立ちます。検討のため、次のように仮定します。

• キャッシュ行: 32 バイト（非常に一般的なサイズ）
• 頂点の形式は次のように構成されます。
  • 位置座標: vec3<float32> = 12 バイト
  • 標準座標: vec3<float32> = 12 バイト
  • UV 座標: vec2<float32> = 8 バイト
  • 合計サイズ = 32 バイト

GPU は、ビニングのためにメモリからデータをフェッチすると、操作対象として 32 バイトのキャッシュ行を取得します。頂点ストリーム分割を使用しない場合、実際にはこのキャッシュ行の最初の 12 バイトのみがビニングに使用され、残りの 20 バイトは次の頂点をフェッチするときに破棄されます。頂点ストリーム分割を使用する場合、頂点位置はメモリ内で連続しているため、32 バイトのチャンクが取得されてキャッシュに保存されるとき、実際には、さらにフェッチを行うためにメインメモリに戻る前に操作する 2 つの頂点位置がまるごと含まれることになります。つまり、2 倍の改善効果が得られます。

さらに、頂点ストリーム分割と頂点圧縮を組み合わせると、1 つの頂点位置のサイズは 6 バイトに縮小されます。したがって、システムメモリから取得された 32 バイトの単一のキャッシュ行は、操作対象の頂点位置をまるごと 5 つ含むことになります。つまり、5 倍の改善効果が得られます。

頂点ストリーム分割の結果

• 頂点のメモリ読み取り帯域幅:
  • ビニング: 27 GB/秒から 6.5 GB/秒に
  • レンダリング: 4.5 GB/秒から 4.5 GB/秒に
• 頂点のフェッチ ストール:
  • ビンニング: 40% から 0% に
  • レンダリング: 90% から 90% に
• 頂点ごとの平均バイト数:
  • ビニング: 48 バイトから 12 バイトに
  • レンダリング: 52 バイトから 52 バイトに

図 5: 分割されていない頂点ストリームの Android GPU Inspector ビュー

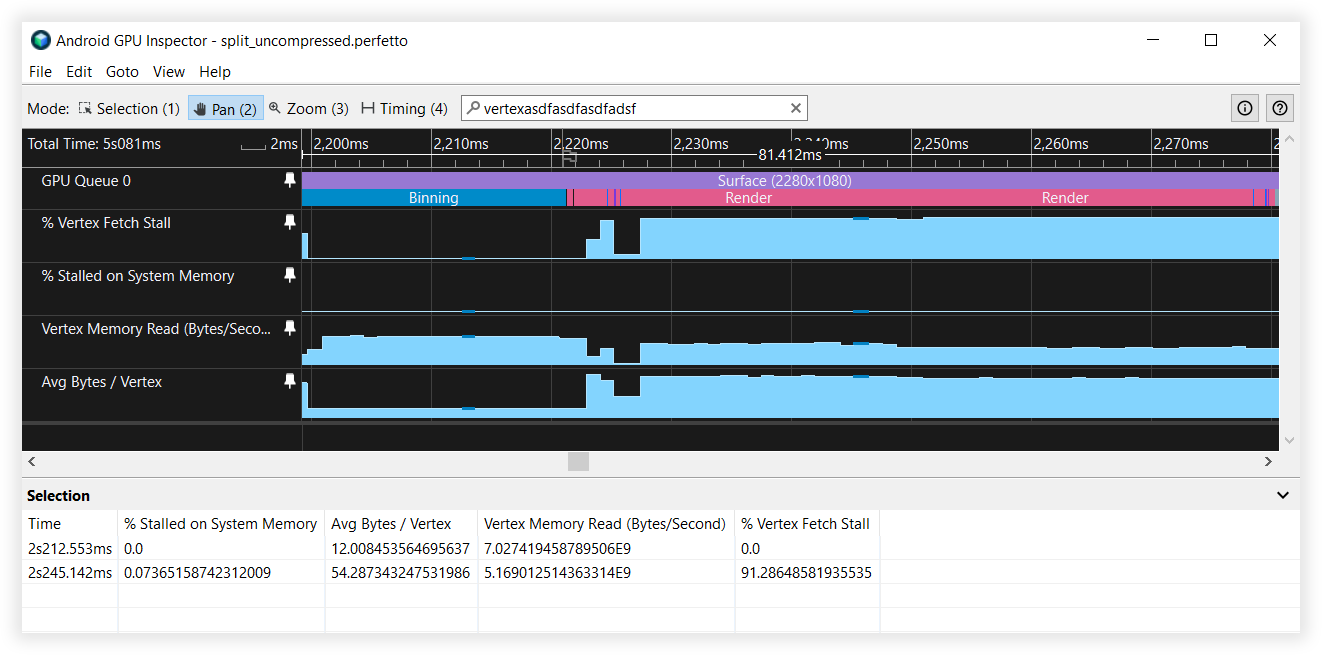
図 6: 分割された頂点ストリームの Android GPU Inspector ビュー

圧縮と分割を組み合わせた結果

• 頂点のメモリ読み取り帯域幅:
  • ビニング: 25 GB/秒から 4.5 GB/秒に
  • レンダリング: 4.5 GB/秒から 1.7 GB/秒に
• 頂点のフェッチ ストール:
  • ビニング: 41% から 0% に
  • レンダリング: 90% から 90% に
• 頂点ごとの平均バイト数:
  • ビニング: 48 バイトから 8 バイトに
  • レンダリング: 52 バイトから 19 バイトに

図 7: 分割および圧縮されていない頂点ストリームの Android GPU Inspector ビュー

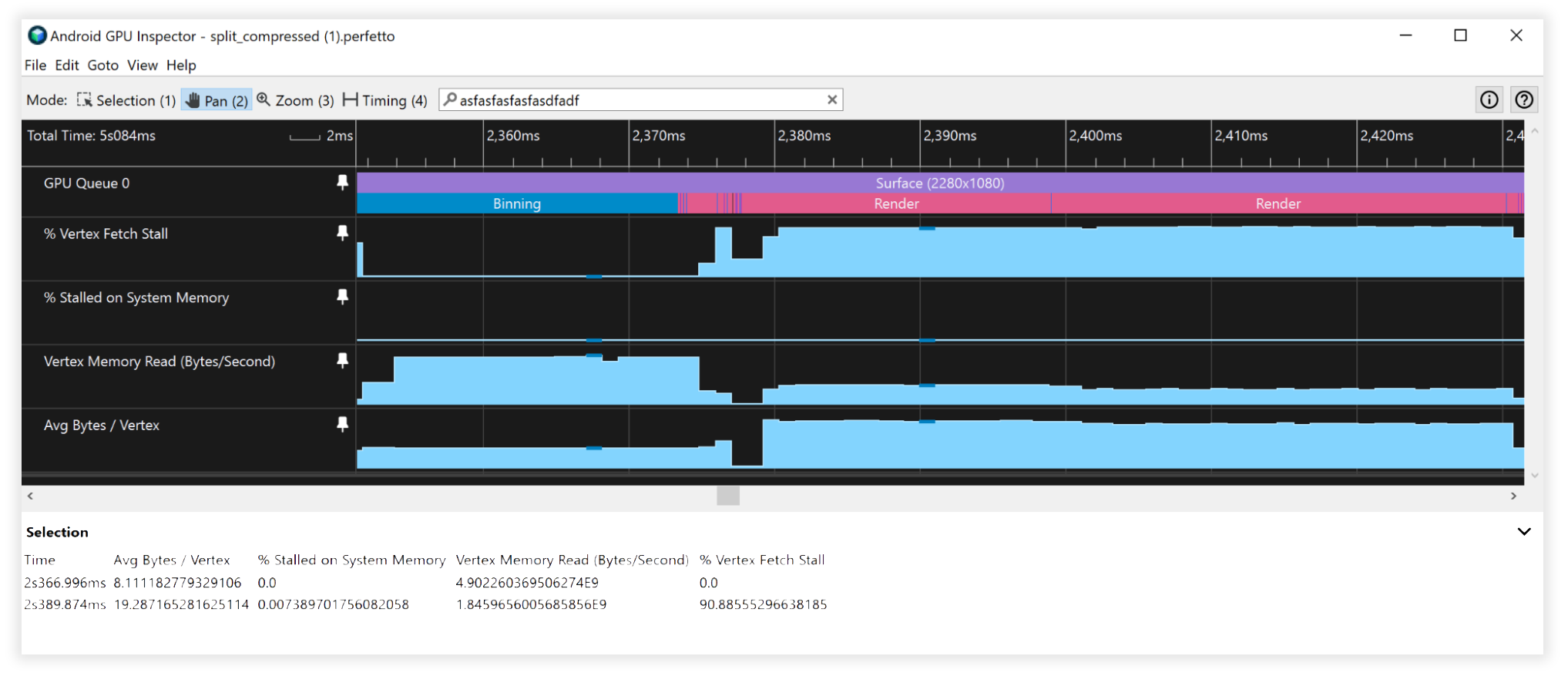
図 8: 分割および圧縮された頂点ストリームの Android GPU Inspector ビュー

その他の考慮事項

16 ビットと 32 ビットのインデックス バッファデータ

• 常に 16 ビット インデックス バッファに収まるようにメッシュを（最大 65,536 個の一意の頂点に）分割 / チャンクします。これは、モバイル上のインデックス付きレンダリングに役立ちます。頂点データのフェッチは低コストで、消費電力が低下するからです。

サポートされていない頂点バッファ属性形式

• SSCALED 頂点形式はモバイルでは広範にサポートされておらず、ハードウェア サポートがない場合は、これをエミュレートしようとするドライバでコストのかかるパフォーマンスのトレードオフが発生する可能性があります。常に SNORM の使用を検討してください。その場合、解凍に要する ALU コストはごくわずかです。