無論應用程式是否包含 2D 使用者介面或開放世界的大型 3D 遊戲,好的頂點資料配置和壓縮都是任何圖像應用程式不可或缺的要素。針對幾十種熱門 Android 遊戲使用 Android GPU 檢查器的影格分析器進行內部測試後發現,頂點資料管理仍有許多改善的空間。觀察發現,頂點資料針對所有頂點屬性使用具有完整精確度的 32 位元浮點值,以及使用具有完全交錯屬性格式結構陣列的頂點緩衝區配置極為常見。
本文說明如何使用下列技術將 Android 應用程式的圖形效能最佳化:
- 頂點壓縮
- 頂點串流分割
導入這些技術可以使頂點記憶體頻寬用量提高 50%、減少 CPU 的記憶體匯流排競爭、降低系統記憶體的遲滯情形,並改善電池續航力,對於開發人員和使用者來說都是雙贏!
此處呈現的所有資料都來自一個範例的靜態場景,其中含有在 Pixel 4 上運作的大約 19,000,000 個頂點:

圖表 1:含有 6 個環和 19m 個頂點的範例場景
頂點壓縮
頂點壓縮是有損壓縮技術的總稱,這項技術會同時在執行階段和在儲存空間中使用有效填充以縮減頂點資料的大小。縮減頂點的大小有許多優點,包括降低 GPU 上的記憶體頻寬 (藉由交易頻寬的運算)、改善快取使用率,以及有助於減緩暫存器溢出的情形。
頂點壓縮的常見方式包括:
- 降低頂點資料屬性的數字精確度 (例如:將 32 位元浮點值降為 16 位元浮點值)
- 代表不同格式的屬性
舉例來說,如果頂點在位置 (vec3)、一般 (vec3) 和紋理座標 (vec2) 使用完整的 32 位元浮點值,將所有這些值替換成 16 位元浮點值,會使頂點大小縮減 50% (平均 32 位元組頂點為 16 位元組)。
頂點位置
頂點位置資料可以從完整精確度 32 位元浮點值,壓縮到絕大多數網格中的 16 位元浮點值,而且幾乎所有行動裝置的硬體皆支援半浮點值。從 float32 到 float16 的轉換函式會如下所示 (改編自這份指南):
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
這個方法設有限制;精確度會隨著距離頂點的起始點越遠而降低,因此對於在空間上極大的網格 (含有超過 1024 元素的頂點) 較不適用。如要解決這個問題,可以將網格分割為數個較小的區塊,將每個區塊置於模型起點中央然後縮放,如此一來每個區塊的所有頂點都會落在 [-1, 1] 的範圍,這個範圍包含了最高的浮點值精確度。壓縮的虛擬程式碼如下所示:
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
您要將縮放比例係數進行烘焙並轉換為模型矩陣,以便在轉譯時將頂點資料解壓縮。提醒您,您不會想使用相同的模式矩陣轉換法向量,因為這些法向量並未套用相同的壓縮。對於法向量,您會需要一個沒有這些解壓縮轉換作業的矩陣,或者也可以使用基本模型矩陣 (可用於法向量),接著將額外的解壓縮轉換套用至著色器內的模型矩陣。範例:
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
另一個方法是使用帶正負號的標準化整數 (SNORM)。SNORM 資料類型使用整數而非浮點來代表 [-1, 1] 之間的值。在位置座標使用 16 位元 SNORM,可讓您省下與 float16 相同的記憶體,而沒有分布不一致的缺點。使用 SNORM 時的建議實作方式如下:
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| 格式 | 大小 | |
|---|---|---|
| 之前 | vec4<float32> |
16 個位元組 |
| 之後 | vec3<float16/SNORM16> |
6 個位元組 |
頂點法向量和切線空間
光照需要使用頂點法向量,較複雜的技術例如法線貼圖,則需要使用切線空間。
切線空間
切線空間是一個座標系統,每個頂點都是由法向量、切線向量和雙切線向量所組成。由於這三個向量通常彼此垂直,因此只需儲存其中兩個向量,即可從頂點著色器中取另外兩個向量的交叉乘積來計算第三個向量。
這些向量通常以 16 位元的浮點值表示,不會有任何明顯可見的視覺保真度失真,因此適合從此處著手!
我們可以進一步使用稱之為 QTangents 的技術進行壓縮,這項技術可以將整個切線空間儲存在單一四元數中。由於四元數可用來表示旋轉,透過將切線空間向量視為 3x3 矩陣的行向量來表示旋轉 (在這個範例中是從模型空間到切線空間),我們即可在這兩者之間轉換!四元數可被視為以 vec4 為資料單位,根據上方連結的文章從切線空間向量轉換到 QTangent,並改編自此處實作的轉換結果如下:
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
四元數將會正規化,您將可以使用 SNORM 進行壓縮。16 位元 SNORM 可提供良好的精確度並節省記憶體用量。8 位元 SNORM 可節省更多記憶體用量,但可能會導致成果變成高度鏡面的材質。可以嘗試上述兩種做法,看看哪個最適合您的資產!四元數的編碼如下所示:
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
如要解碼頂點著色器中的四元數 (改編自此處):
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| 格式 | 大小 | |
|---|---|---|
| 之前 | vec3<float32> + vec3<float32> + vec3<float32> |
36 個位元組 |
| 之後 | vec4<SNORM16> |
8 個位元組 |
僅限法向量
如果只需要儲存法向量,有其他方式可以節省更多記憶體用量,例如使用單位向量的八面體映射,而非笛卡兒座標來壓縮法向量。八面體映射的運作方式,是將單位球面投影到八面體,然後將八面體投影到 2D 平面。因此,您可以只使用兩個數字來表示任何的法向量。這兩個數字可以視為紋理座標,也就是我們將球面投影於其上的 2D 平面「取樣」的座標,可讓我們復原原始向量。這兩個數字之後會儲存在 SNORM8 中。

圖表 2:以視覺化方式呈現八面體映射 (資料來源)
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
在頂點著色器中解壓縮 (以轉換回笛卡兒座標) 代價並不高昂;在大部分現代行動裝置上實作這項技術時,我們並沒有發現任何重大效能降低的情況。頂點著色器中的解壓縮方式如下所示:
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
這個方法也可用來儲存整個切線空間,運用這項技術儲存使用 vec2 的法向量和切線向量<SNORM8>但是,您必須設法儲存雙切線的方向 (這個用於將 UV 座標對映到模型的常見情境)。其中一種做法是將切線向量編碼的元件一律採用正映射,然後在需要反轉雙切線方向時翻轉其符號,並在頂點著色器中加以檢查。
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| 格式 | 大小 | |
|---|---|---|
| 之前 | vec3<float32> |
12 個位元組 |
| 之後 | vec2<SNORM8> |
2 個位元組 |
頂點 UV 座標
用於紋理映射的 UV 座標通常以 32 位元的浮點值儲存。使用 16 位元浮點值加以壓縮會導致精確度問題,使得紋理大於 1024x1024;[0.5, 1.0] 之間的浮點精確度則代表值會增加大於 1 像素!
較佳的做法是使用不帶正負號的標準化整數 (UNORM),特別是 UNORM16;這麽做會使整個紋理座標範圍可平均分布,支援高達 65536x65536 的紋理!這種做法假定紋理座標在每個元素的 [0.0, 1.0] 範圍內,情況可能依網格而異 (例如牆壁可以使用大於 1.0 的環繞紋理座標)。轉換函式會如下所示:
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| 格式 | 大小 | |
|---|---|---|
| 之前 | vec2<float32> |
8 個位元組 |
| 之後 | vec2<UNORM16> |
4 個位元組 |
頂點壓縮結果
這些頂點壓縮技術可減少 66% 的頂點記憶體儲存空間,從 48 個位元組降至 16 個位元組,顯示如下:
- 頂點記憶體讀取頻寬:
- 特徵分塊:27GB/s 至 9GB/s
- 算繪:4.5B/s 到 1.5GB/s
- Vertex Fetch Stalls:
- 特徵分塊:50% 至 0%
- 算繪:90% 到 90%
- 平均位元組/頂點:
- 特徵分塊:48B 至 16B
- 算繪:52B 至 18B
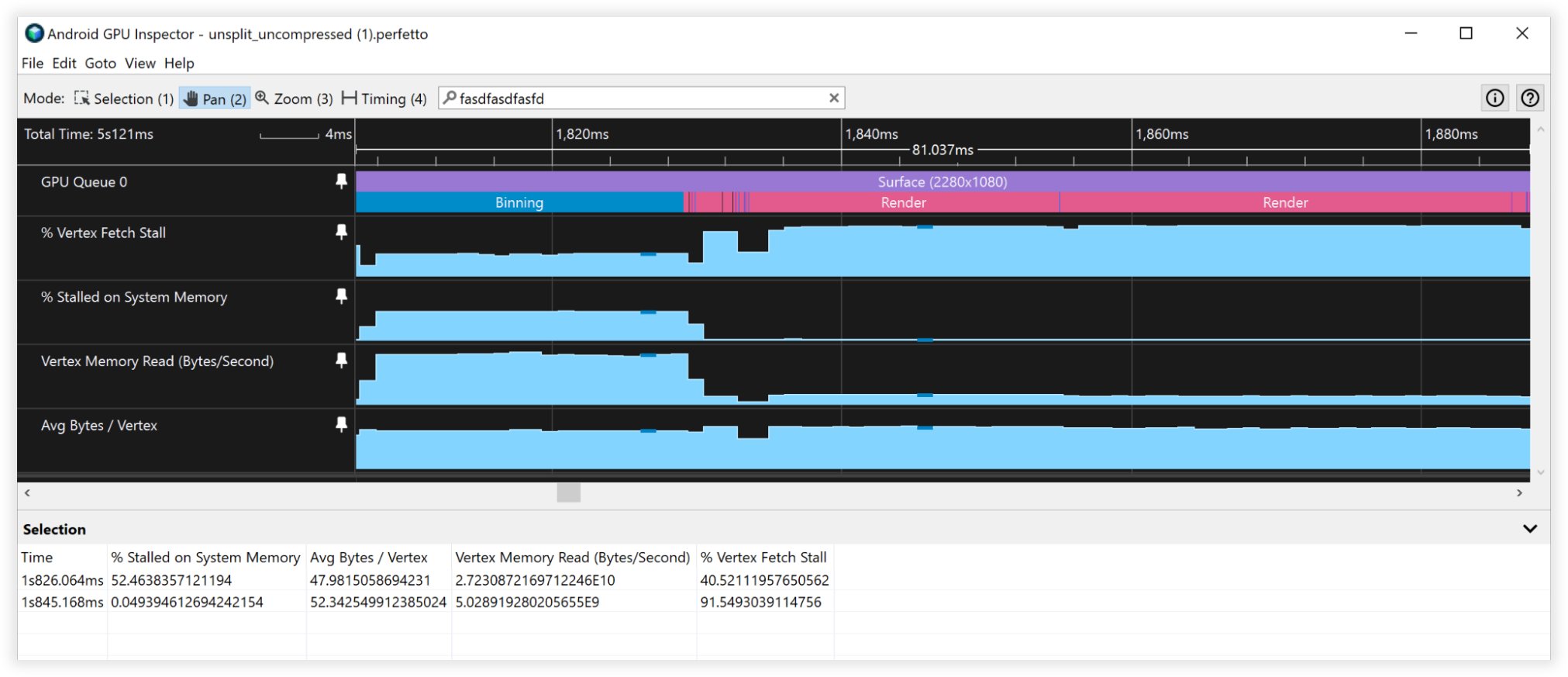
圖表 3:未壓縮頂點的 Android GPU 檢查器檢視畫面
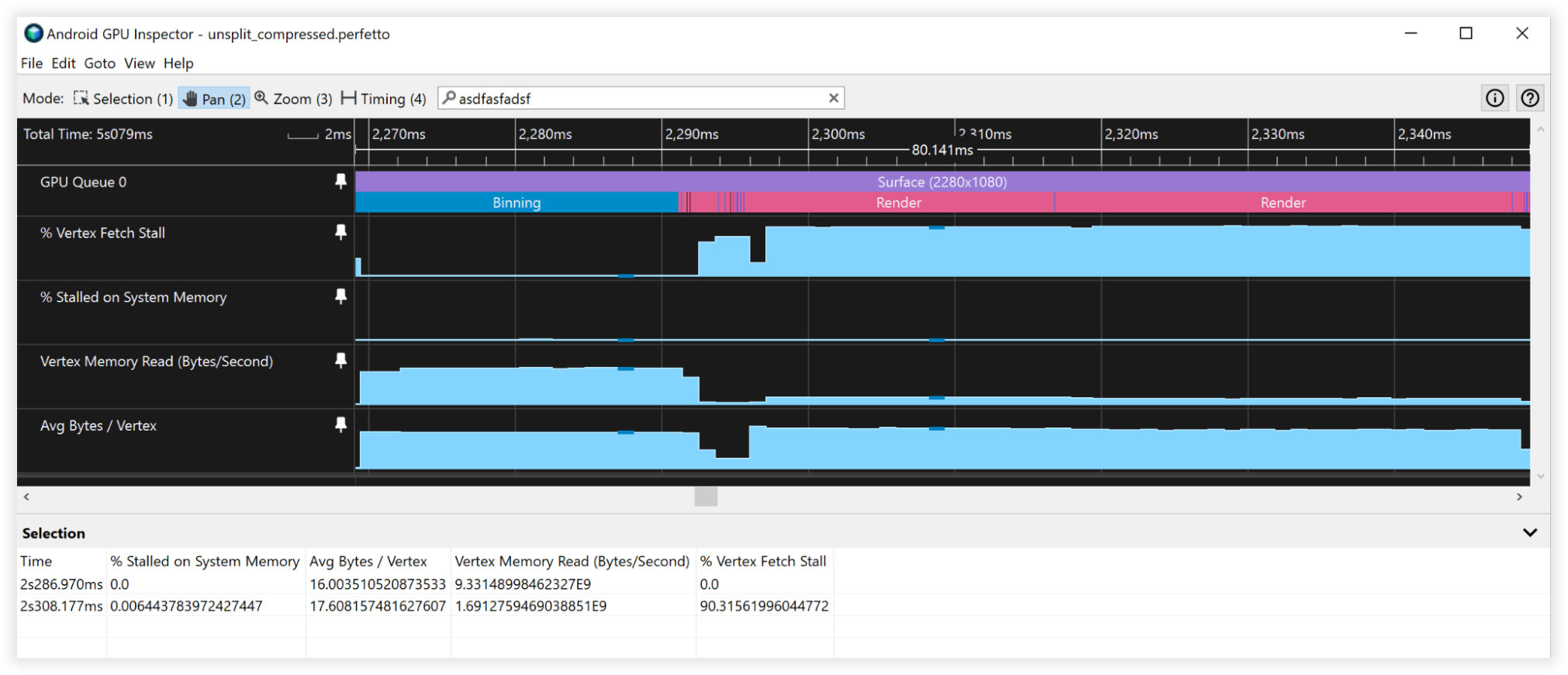
圖表 4:壓縮頂點的 Android GPU 檢查器檢視畫面
頂點串流分割
頂點串流分割會將頂點緩衝區中的資料組織最佳化。這是一種快取效能最佳化,通常對於 Android 裝置中的圖塊式 GPU 會造成差異,特別是在算繪程序的特徵分塊階段。
圖塊式 GPU 會建立著色器,這個著色器可根據所提供的頂點著色器計算正規裝置座標以進行特徵分塊。無論是否肉眼可見,都會先在場景中的每個頂點執行。因此,將頂點位置資料保持在鄰近的記憶體中是一大優勢。這個頂點串流版面配置可以發揮益處的其他地方是供陰影傳遞。通常只需要位置資料即可計算陰影並計算深度延遲,這項技術通常用於控制台/電腦算繪;這個頂點串流版面配置為多個類別的算繪引擎帶來益處!
串流分割牽涉到設定頂點緩衝區,透過頂點位置資料的相鄰部分,以及包含交錯頂點屬性的另一部分來設定。多數應用程式通常會將緩衝區設定為完全與所有屬性交錯。這張圖片說明了其中的差異:
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
查看 GPU 擷取頂點資料的方式,如何幫助我們瞭解串流分割的優點。假設引數為:
- 32 位元組快取行 (十分常見的大小)
- 頂點格式包括:
- Position, vec3<float32> = 12 bytes
- Normal vec3<float32> = 12 bytes
- UV coordinates vec2<float32> = 8 bytes
- Total size = 32 bytes
GPU 從記憶體為特徵分塊擷取資料時,將會提取 32 個位元組的快取行來執行。如果沒有頂點串流分割,則只會使用此快取行的前 12 個位元組進行特徵分塊,並在擷取下一個頂點時捨棄其餘的 20 個位元組。使用頂點串流分割時,頂點位置會在記憶體中相鄰,因此當 32 位元組的區塊被提取到快取中時,在必須返回主記憶體擷取更多資料之前,實際上會包含 2 個完整的頂點位置以供運作,提升了 2 倍之多!
現在,如果將頂點串流分割與頂點壓縮結合,單一頂點位置的大小將縮減至 6 個位元組,因此從系統記憶體中提取的單一 32 位元組快取行將有 5 個完整的頂點位置可供運作,提升了 5 倍之多!
頂點串流分割結果
- 頂點記憶體讀取頻寬:
- 特徵分塊:27GB/s 至 6.5GB/s
- 算繪:4.5GB/s 到 4.5GB/s
- Vertex Fetch Stalls:
- 特徵分塊:40% 至 0%
- 算繪:90% 到 90%
- 平均位元組/頂點:
- 特徵分塊:48B 至 12B
- 算繪:52B 至 52B

圖表 5:未分割頂點串流的 Android GPU 檢查器檢視畫面
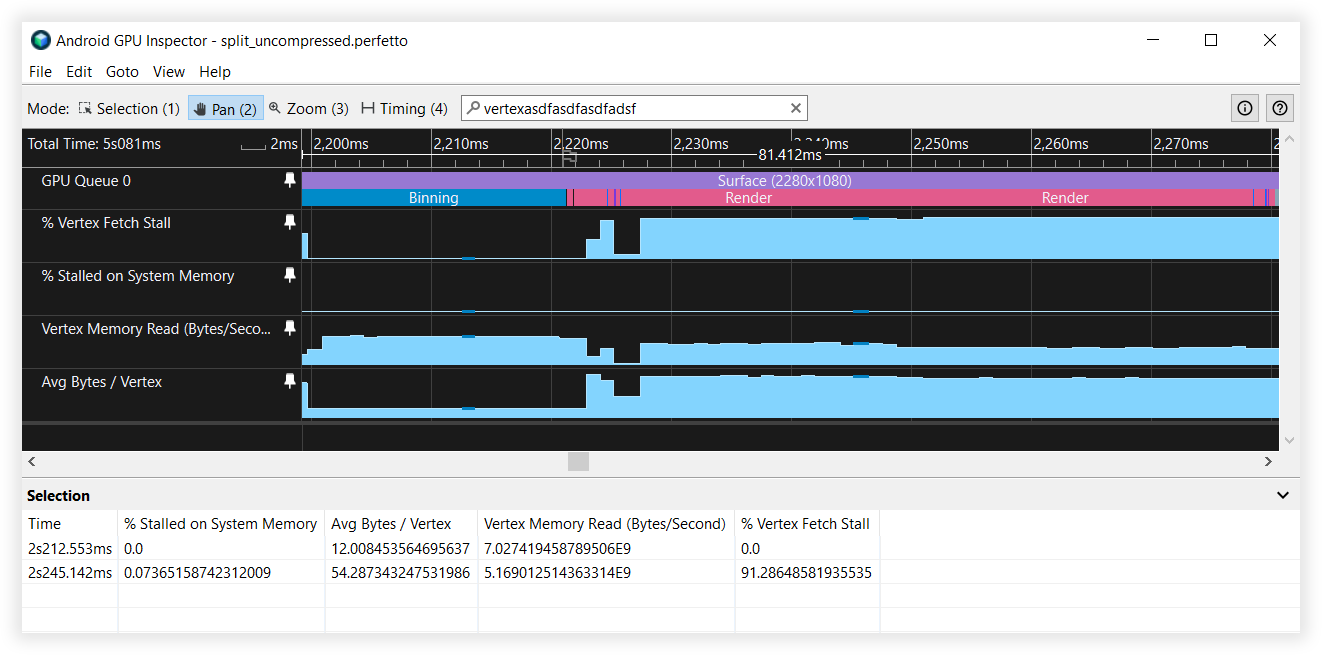
圖表 6:已分割頂點串流的 Android GPU 檢查器檢視畫面
複合結果
- 頂點記憶體讀取頻寬:
- 特徵分塊:25GB/s 至 4.5GB/s
- 算繪:4.5GB/s 到 1.7GB/s
- Vertex Fetch Stalls:
- 特徵分塊:41% 至 0%
- 算繪:90% 到 90%
- 平均位元組/頂點:
- 特徵分塊:48B 至 8B
- 算繪:52B 至 19B

圖表 7:含有未分割、未壓縮頂點串流的 Android GPU 檢查器檢視畫面
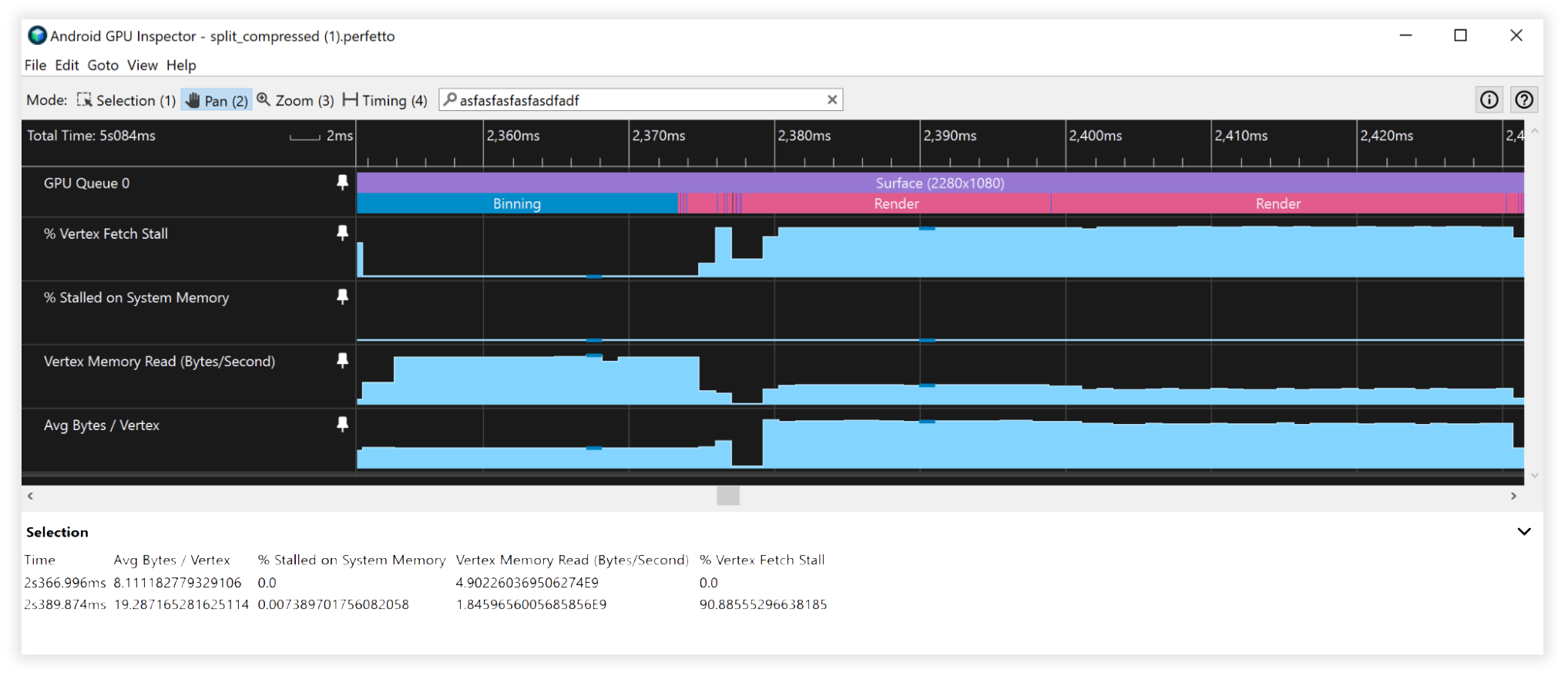
圖表 8:顯示已分割、壓縮頂點串流的 Android GPU 檢查器檢視畫面
其他考量
16 與 32 位元的索引緩衝區資料
- 一律分割/區塊網格,使其與 16 位元索引緩衝區相容 (最多 65536 個不重複頂點)。這樣將有助於行動裝置上已建立索引的算繪,因為擷取頂點資料較為便宜且耗電量較低。
不支援的頂點緩衝區屬性格式
- 行動裝置未廣泛支援 SSCALED 頂點格式,且使用時如果嘗試模擬該格式,可能會在未擁有硬體支援的驅動程式中造成效能大量損失。一律使用 SNORM,並承擔可忽略的 ALU 成本以進行解壓縮。
