Zarządzanie danymi Vertex

Odpowiedni układ i kompresja danych wierzchołkowych mają kluczowe znaczenie dla wydajności każdej aplikacji graficznej, niezależnie od tego, czy składa się ona z interfejsów 2D czy jest dużą grą 3D w otwartym świecie. Wewnętrzne testy narzędzia Frame Profiler – narzędzia Android GPU Inspector w dziesiątkach najpopularniejszych gier na Androida pokazują, że wiele można zrobić, aby poprawić zarządzanie danymi wierzchołków. Zaobserwowaliśmy, że dane wierzchołków często korzystają z pełnej dokładności, 32-bitowych wartości zmiennoprzecinkowych dla wszystkich atrybutów wierzchołków oraz w układzie bufora wierzchołków, który wykorzystuje tablicę struktur sformatowanych z w pełni przeplatanymi atrybutami.

W tym artykule opisujemy, jak zoptymalizować wydajność grafiki w aplikacji na Androida przy użyciu tych technik:

• Kompresja Vertex
• Dzielenie Vertex Stream

Wdrożenie tych technik może poprawić wykorzystanie przepustowości pamięci przez wierzchołki nawet o 50%, ograniczyć rywalizację o magistralię pamięci z procesorem, ograniczyć zatrzymania się w pamięci systemowej i wydłużyć czas pracy na baterii. Wszystkie te korzyści są korzystne zarówno dla programistów, jak i użytkowników.

Wszystkie przedstawione dane pochodzą z przykładowej sceny statycznej zawierającej ok. 19 milionów wierzchołków na Pixelu 4:

Ilustracja 1: przykładowa scena z 6 pierścieniami i 19-metrowymi wierzchołkami

Kompresja Vertex

Vertex Compression to ogólny termin dotyczący technik kompresji stratnej, które użyj wydajnego pakowania, aby zmniejszyć rozmiar danych wierzchołkowych zarówno w czasie działania, jak i w pamięci. Zmniejszenie rozmiaru wierzchołków ma kilka zalet, w tym zmniejszenie przepustowości pamięci GPU (przez zamianę mocy obliczeniowej na przepustowość), poprawę wykorzystania pamięci podręcznej i potencjalne zmniejszenie ryzyka wystąpienia rejestrów.

Typowe metody kompresji Vertex:

• Zmniejszanie precyzji liczbowej atrybutów danych wierzchołków (np. 32-bitowa liczba zmiennoprzecinkowa na 16-bitową liczbę zmiennoprzecinkową)
• Prezentowanie atrybutów w różnych formatach

Jeśli na przykład wierzchołek korzysta z pełnych 32-bitowych liczb zmiennoprzecinkowych pozycji (vec3), normalnych (vec3) i współrzędnych tekstury (vec2), zastąpienie ich wszystkimi 16-bitowymi liczbami zmiennoprzecinkowymi zmniejszy rozmiar wierzchołków o 50% (16 bajtów przy 32-bajtowym wierzchołku).

Pozycje wierzchołków

Dane o pozycji wierzchołka mogą być kompresowane od pełnej dokładności 32-bitowej liczby zmiennoprzecinkowych do połowy dokładnych, 16-bitowych wartości zmiennoprzecinkowych w większości sieci typu mesh. Połówki zmiennoprzecinkowe są obsługiwane przez sprzęt na prawie wszystkich urządzeniach mobilnych. Funkcja konwersji zmieniająca się z float32 na float16 wygląda tak (dostosowana na podstawie tego przewodnika):

uint16_t f32_to_f16(float f) {
  uint32_t x = (uint32_t)f;
  uint32_t sign = (unsigned short)(x >> 31);
  uint32_t mantissa;
  uint32_t exp;
  uint16_t hf;

  mantissa = x & ((1 << 23) - 1);
  exp = x & (0xFF << 23);
  if (exp >= 0x47800000) {
    // check if the original number is a NaN
    if (mantissa && (exp == (0xFF << 23))) {
      // single precision NaN
      mantissa = (1 << 23) - 1;
    } else {
      // half-float will be Inf
      mantissa = 0;
    }
    hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
         (uint16_t)(mantissa >> 13);
  }
  // check if exponent is <= -15
  else if (exp <= 0x38000000) {
    hf = 0;  // too small to be represented
  } else {
    hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
         (uint16_t)(mantissa >> 13);
  }

  return hf;
}

To podejście ma pewne ograniczenia. precyzja pogarsza się w miarę oddalania się wierzchołka od punktu początkowego, przez co staje się mniej odpowiednia dla siatek o bardzo dużych przestrzennych wierzchołkach (wierzchołki z elementami przekraczającymi 1024). Aby rozwiązać ten problem, podziel siatkę na mniejsze fragmenty, wyśrodkuj każdy z nich wokół punktu początkowego modelu i przeskaluj tak, aby wszystkie wierzchołki każdego fragmentu pasowały do zakresu [-1, 1], który zapewnia największą precyzję dla wartości liczb zmiennoprzecinkowych. Pseudokod kompresji wygląda tak:

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));

Wypalasz współczynnik skali i przesunięcie do macierzy modeli, aby zdekompresować dane wierzchołków podczas renderowania. Pamiętaj, że nie należy używać tej samej macierzy modelu do przekształcania normalnych, ponieważ nie zastosowano do nich takiej samej kompresji. W przypadku normalnych funkcji potrzebujesz macierzy bez tych przekształceń dekompresyjnych. Możesz też użyć macierzy modelu podstawowego (którego możesz użyć w przypadku norm), a następnie zastosować dodatkowe przekształcenia dekompresyjne do macierzy modeli w ramach cieniowania. Przykład:

vec3 in in_pos;

void main() {
   ...
   // bounding box data packed into uniform buffer
   vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
   gl_Position = proj * view * model * decompress_pos;
}

Innym sposobem jest użycie znormalizowanych liczb całkowitych (SNORM). W typach danych SNORM wartości z zakresu od [–1 do 1] są przedstawiane za pomocą liczb całkowitych, a nie zmiennoprzecinkowych. Użycie 16-bitowego parametru SNORM do określania pozycji zapewnia tyle samo oszczędności pamięci co w przypadku typu float16 (bez wad niejednolitych rozkładów). Zalecana przez nas implementacja w przypadku SNORM wygląda tak:

const int BITS = 16

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   // float to integer value conversion
   p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1) 

	Format	Rozmiar
Przed	vec4<float32>	16 bajtów
Po	vec3<float16/SNORM16>	6 bajtów

Normalne i styczna wierzchołków

Oświetlenie wymaga zastosowania wartości Vertex Normals, a w przypadku bardziej skomplikowanych technik, takich jak tworzenie normalnego mapowania, potrzebna jest przestrzeń styczna.

Przestrzeń styczna

Przestrzeń styczna to układ współrzędnych, w którym każdy wierzchołek składa się z wektora normalnego, tangensa i bitangenta. Ponieważ te trzy wektory są zwykle ortogonalne, wystarczy zapisać tylko dwa z nich i wyliczyć trzeci, analizując iloczyn krzyżowy pozostałych dwóch w cieniu wierzchołkowym.

Takie wektory można zwykle przedstawić za pomocą 16-bitowych znaków zmiennoprzecinkowych bez utraty jakości wizualnej. To dobry punkt wyjścia.

Możemy jeszcze bardziej skompresować dane za pomocą metody znanej jako QTangents, która przechowuje całą styczną przestrzeń w jednym kwartionie. Ze względu na to, że kwantiony mogą być stosowane do przedstawiania obrotów, traktując styczne wektory przestrzeni kosmicznej jako wektory kolumn macierzy 3 x 3 reprezentujące obrót (w tym przypadku z przestrzeni modelu do przestrzeni stycznej), możemy dokonać konwersji między nimi. Kwaternion można traktować jako dane zgodne z wartością vec4, a przekształcenie z tangensowych wektorów kosmicznych w QTangent na podstawie artykułu, do którego link znajdziesz powyżej, i dostosowanie na podstawie implementacji wygląda tak:

const int BITS = 16

quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
   mat3 tbn = {normal, tangent, bitangent};
   quaternion qTangent(tbn);
   qTangent.normalize();

   //Make sure QTangent is always positive
   if (qTangent.w < 0)
       qTangent = -qTangent;

   const float bias = 1.0 / (2^(BITS - 1) - 1);

   //Because '-0' sign information is lost when using integers,
   //we need to apply a "bias"; while making sure the Quaternion
   //stays normalized.
   // ** Also our shaders assume qTangent.w is never 0. **
   if (qTangent.w < bias) {
       Real normFactor = Math::Sqrt( 1 - bias * bias );
       qTangent.w = bias;
       qTangent.x *= normFactor;
       qTangent.y *= normFactor;
       qTangent.z *= normFactor;
   }

   //If it's reflected, then make sure .w is negative.
   vec3 naturalBinormal = cross_product(tangent, normal);
   if (dot_product(naturalBinormal, binormal) <= 0)
       qTangent = -qTangent;
   return qTangent;
}

Kwartionon zostanie znormalizowany i będzie można go skompresować za pomocą funkcji SNORM. 16-bitowe układy SNORM zapewniają dużą precyzję i oszczędzanie pamięci. 8-bitowe układy SNORM mogą zapewnić jeszcze większe oszczędności, ale mogą powodować artefakty w materiałach bardzo okrągłych. Możesz wypróbować oba i zobaczyć, co sprawdza się najlepiej w przypadku Twoich zasobów. Kodowanie kwartionu wygląda tak:

for each vertex v in mesh:
   quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
   // Once we have the quaternion we can compress it
   res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);

Aby zdekodować kwartion w programie cieniowania wierzchołków (dostosowany tutaj):

vec3 xAxis( vec4 qQuat )
{
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwy = fTy * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxy = fTy * qQuat.x;
  float fTxz = fTz * qQuat.x;
  float fTyy = fTy * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}

vec3 yAxis( vec4 qQuat )
{
  float fTx  = 2.0 * qQuat.x;
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwx = fTx * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxx = fTx * qQuat.x;
  float fTxy = fTy * qQuat.x;
  float fTyz = fTz * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}

void main() {
  vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
  vec3 normal = xAxis(qtangent);
  vec3 tangent = yAxis(qtangent);
  float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
  vec3 binormal = cross(normal, tangent) * biNormalReflection;
  ...
}

	Format	Rozmiar
Przed	vec3<float32> + vec3<float32> + vec3<float32>	36 bajtów
Po	vec4<SNORM16>	8 bajtów

Tylko normalne

Jeśli musisz przechowywać tylko zwykłe wektory, możesz skorzystać z innego podejścia, które może przynieść większe oszczędności. Użyj mapowania ośmiościanowego wektorów jednostkowych zamiast współrzędnych kartezjańskich do skompresowania wektora normalnego. Mapowanie ośmiościenne polega na rzutowaniu jednostki kuli na ośmiościan, a następnie rzutowaniu ośmiościanu w dół na płaszczyznę 2D. W rezultacie możesz przedstawić dowolny wektor normalny przy użyciu tylko dwóch liczb. Te dwie liczby można traktować jak współrzędne tekstury używane do „próbkowania” płaszczyzny 2D, na którą rzutowaliśmy kulę, co pozwala nam odzyskać pierwotny wektor. Te 2 numery można zapisać w raporcie SNORM8.

Ilustracja 2: Zwizualizowane mapowanie ośmiościowe (źródło)

const int BITS = 8

// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
  float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
  vec2 res;
  if (n.z < 0.0) {
    res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
    res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
  } else {
    res.x = n.x * invL1Norm;
    res.y = n.y * invL1Norm;
  }
  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

Dekompresja za pomocą cieniowania wierzchołków (konwertowanie z powrotem do współrzędnych kartezjańskich) jest niedroga. na większości nowoczesnych urządzeń mobilnych nie zauważyliśmy znaczącego spadku wydajności po wdrożeniu tej metody. Dekompresja w cieniującym wierzchołków:

//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
  vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
  float t = max(-v.z, 0.0);
  v.xy += t * -sign(v.xy);
  return v;

W ten sposób można również zapisać całą przestrzeń tangensów, wykorzystując tę metodę do przechowywania wektorów normalnych i tangensowych przy użyciu funkcji vec2<SNORM8> ale trzeba znaleźć sposób zapisania kierunku bitangentu (potrzebny jest typowy scenariusz, w którym są odbicia lustrzane współrzędnych UV na modelu). Jednym ze sposobów wdrożenia tego rozwiązania jest zmapowanie komponentu kodowania wektorów stycznych na wartość dodatnią, a następnie odwrócenie znaku, jeśli trzeba odwrócić kierunek bitangentu i sprawdzenie tego za pomocą cieniowania wierzchołkowego:

const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)

// Compressing
for each normal n in mesh:
  //encode to octahedron, result in range [-1, 1]
  vec2 res = vec_to_oct(n);

  // map y to always be positive
  res.y = res.y * 0.5 + 0.5;

  // add a bias so that y is never 0 (sign in the vertex shader)
  if (res.y < bias)
    res.y = bias;

  // Apply the sign of the binormal to y, which was computed elsewhere
  if (binormal_sign < 0)
    res.y *= -1;

  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);

	Format	Rozmiar
Przed	vec3<float32>	12 bajtów
Po	vec2<SNORM8>	2 bajty

Współrzędne UV Vertex

Współrzędne UV używane między innymi do mapowania tekstur są zwykle przechowywane za pomocą 32-bitowych liczb zmiennoprzecinkowych. Skompresowanie ich za pomocą 16-bitowych liczb zmiennoprzecinkowych powoduje problemy z precyzją w przypadku tekstur większych niż 1024 x 1024. precyzja zmiennoprzecinkowa między [0,5 i 1,0] oznacza, że wartości będą rosnąć o co najmniej 1 piksel.

Lepszym podejściem jest użycie znormalizowanych liczb całkowitych bez znaku (UNORM), a w szczególności UNORM16. zapewnia to jednolity rozkład w całym zakresie współrzędnych tekstury, obsługując tekstury do 65 536 x 65 536. Przy założeniu, że współrzędne tekstury mieszczą się w zakresie [0,0, 1,0] na element, co może nie mieć miejsca w zależności od siatki (np. ściany mogą używać współrzędnych tekstury zawijania, które są większe niż 1,0). Należy o tym pamiętać, analizując tę technikę. Funkcja konwersji będzie wyglądać tak:

const int BITS = 16

for each vertex_uv V in mesh:
  V *= clamp(2^BITS - 1, 0, 2^BITS - 1);  // float to integer value conversion

	Format	Rozmiar
Przed	vec2<float32>	8 bajtów
Po	vec2<UNORM16>	4 bajty

Wyniki kompresji Vertex

Te techniki kompresji wierzchołków pozwoliły zmniejszyć ilość pamięci masowej na wierzchołkach o 66%, zamiast z 48 do 16 bajtów. Efekt:

• Przepustowość odczytu pamięci Vertex:
  • Łączenie: od 27 GB/s do 9 GB/s
  • Renderowanie: 4,5 B/s do 1,5 GB/s
• Ograniczenia pobierania Vertex:
  • binarny: 50% do 0%
  • Renderowanie: 90–90%
• Średnia liczba bajtów/Vertex:
  • binowanie: od 48 B do 16 mld,
  • Renderowanie: 52–18 mld

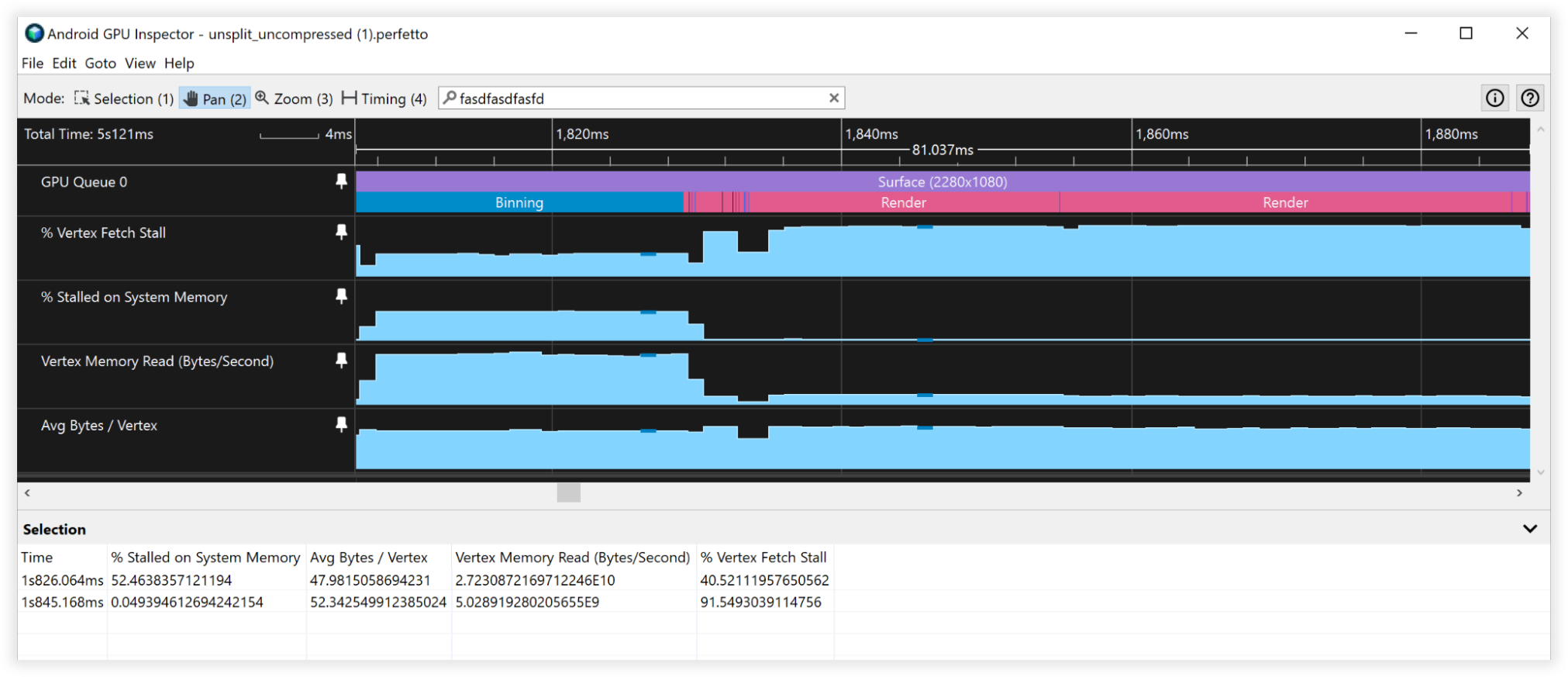
Ilustracja 3. Widok Inspektora GPU na Androidzie z nieskompresowanymi wierzchołkami

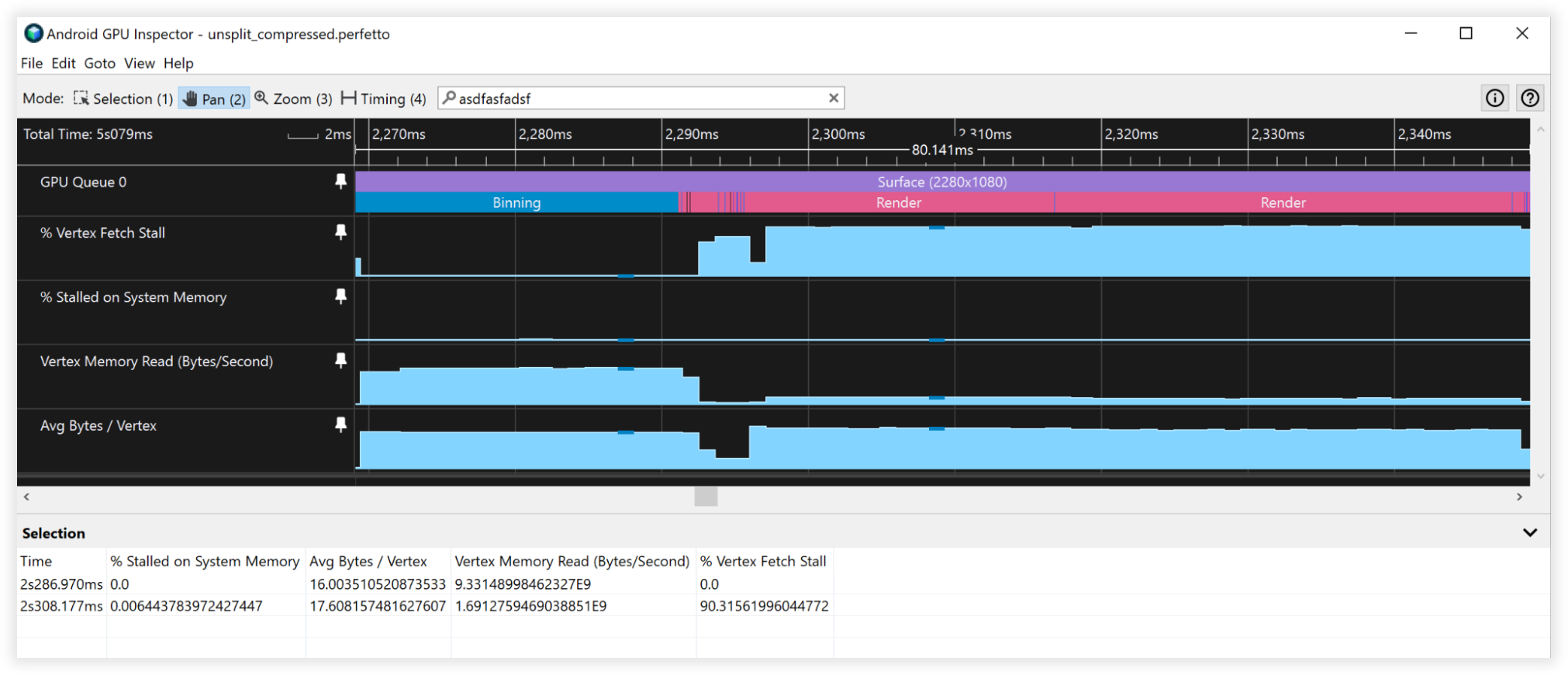
Ilustracja 4. Widok skompresowanych wierzchołków w Inspektorze GPU na Androidzie

Dzielenie Vertex Stream

Dzielenie strumieni Vertex optymalizuje organizację danych w buforze wierzchołków. Jest to optymalizacja wydajności pamięci podręcznej, która ma znaczenie w przypadku układów GPU opartych na kafelkach zazwyczaj spotykanych na urządzeniach z Androidem, zwłaszcza na etapie tworzenia powiązania w procesie renderowania.

Procesory graficzne oparte na kafelkach tworzą cieniowanie, które oblicza znormalizowane współrzędne urządzenia na podstawie podanego cieniowania wierzchołków potrzebnego do tworzenia powiązań. Najpierw wykonuje się go na każdym wierzchołku sceny niezależnie od tego, czy jest widoczny. Zapewnienie ciągłości danych o położeniu wierzchołków w pamięci stanowi więc duży plus. Inne miejsca, w których ten układ wierzchołkowy może być korzystny w przypadku przejść cieni, wymaga zwykle jedynie danych o pozycji do obliczeń cieni, a także danych o położeniu, które są stosowane zwykle w przypadku renderowania na konsolach i komputerach. ten układ strumienia wierzchołkowego może być korzystny dla wielu klas silnika renderowania.

Dzielenie strumienia obejmuje skonfigurowanie bufora wierzchołków z przyległą sekcją danych o położeniu wierzchołków oraz inną sekcję zawierającą przeplatane atrybuty wierzchołków. Większość aplikacji zwykle konfiguruje bufory w pełni z wykorzystaniem wszystkich atrybutów. Ten obraz pokazuje różnicę:

Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|

After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|

Przyglądając się temu, jak GPU pobiera dane wierzchołkowe, możemy lepiej poznać zalety podział strumienia danych z sieci. Zakładając:

• 32-bajtowe wiersze pamięci podręcznej (dosyć typowy rozmiar)
• Format Vertex składający się z:
  • Pozycja, vec3<float32> = 12 bajtów
  • Normalne vec3<float32> = 12 bajtów
  • Współrzędne UV vec2<float32> = 8 bajtów
  • Łączny rozmiar = 32 bajty

Gdy GPU pobiera dane z pamięci w celu powiązania, pobiera do działania 32-bajtowy wiersz pamięci podręcznej. Bez podziału strumienia wierzchołków do powiązania wykorzysta tylko pierwsze 12 bajtów z tego wiersza pamięci podręcznej, a pozostałe 20 bajtów zostanie odrzuconych podczas pobierania kolejnego wierzchołka. W przypadku dzielenia strumienia wierzchołków położenia wierzchołków są przylegające w pamięci, więc gdy ten 32-bajtowy fragment zostanie pobrany do pamięci podręcznej, będzie zawierał 2 pełne położenia wierzchołków do działania, zanim trzeba będzie wrócić do pamięci głównej w celu pobrania większej ilości danych – to 2 razy lepsze rozwiązanie.

Teraz, gdy połączymy dzielenie strumienia wierzchołków z kompresją wierzchołkową, zmniejszymy rozmiar pojedynczego wierzchołka do 6 bajtów. Dzięki temu pojedyncza 32-bajtowa linia pamięci podręcznej pobierana z pamięci systemowej będzie miała do działania 5 całych pozycji wierzchołków – to 5-krotne ulepszenie.

Wyniki podziału Vertex Stream

• Przepustowość odczytu pamięci Vertex:
  • Łączenie: od 27 GB/s do 6,5 GB/s
  • Renderowanie: 4,5 GB/s do 4,5 GB/s
• Ograniczenia pobierania Vertex:
  • binarny: 40% do 0%
  • Renderowanie: 90–90%
• Średnia liczba bajtów na wertex:
  • binowanie: od 48 B do 12 mld,
  • Renderowanie: 52–52 B

Ilustracja 5. Widok Inspektora GPU na Androidzie:niepodzielone strumienie wierzchołków

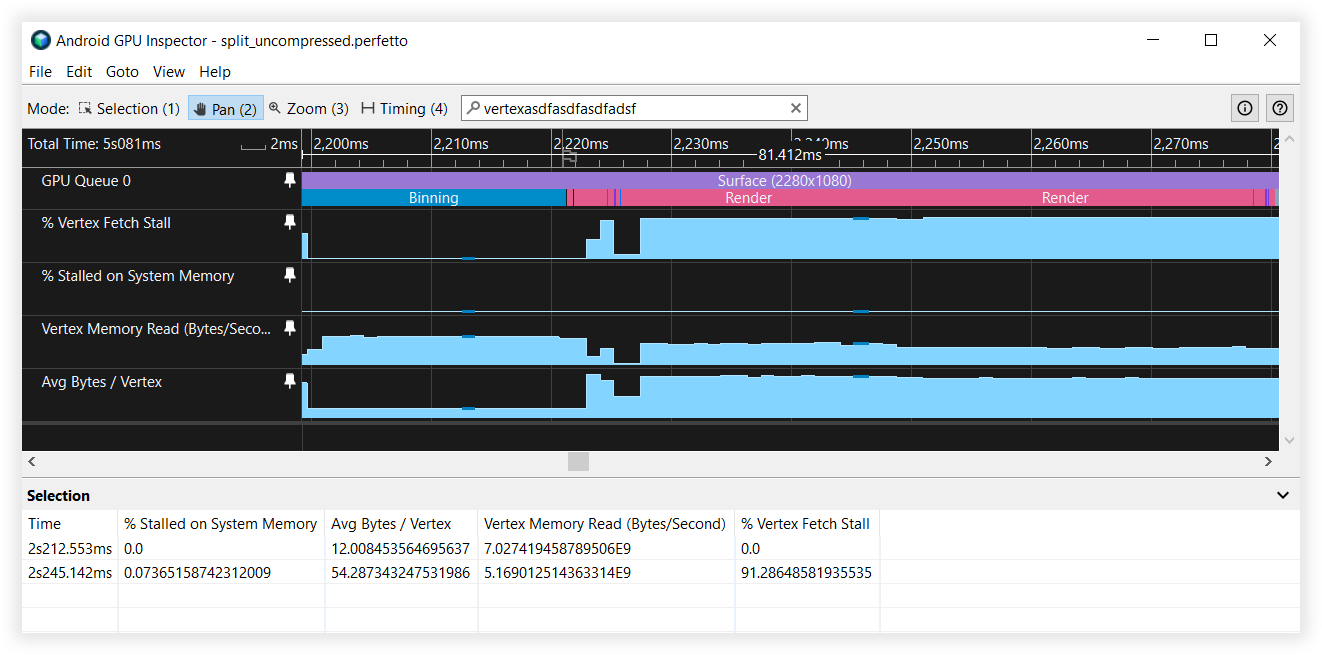
Ilustracja 6. Widok Inspektora GPU na Androidzie:podzielone strumienie wierzchołków

Wyniki złożone

• Przepustowość odczytu pamięci Vertex:
  • Łączenie: od 25 GB/s do 4,5 GB/s
  • Renderowanie: 4,5 GB/s do 1,7 GB/s
• Ograniczenia pobierania Vertex:
  • binarny: 41% do 0%
  • Renderowanie: 90–90%
• Średnia liczba bajtów na wertex:
  • Powiązanie: od 48 B do 8 mld
  • Renderowanie: 52–19 B

Ilustracja 7. Widok Inspektora GPU na Androidzie z niepodzielonymi, nieskompresowanymi strumieniami wierzchołków

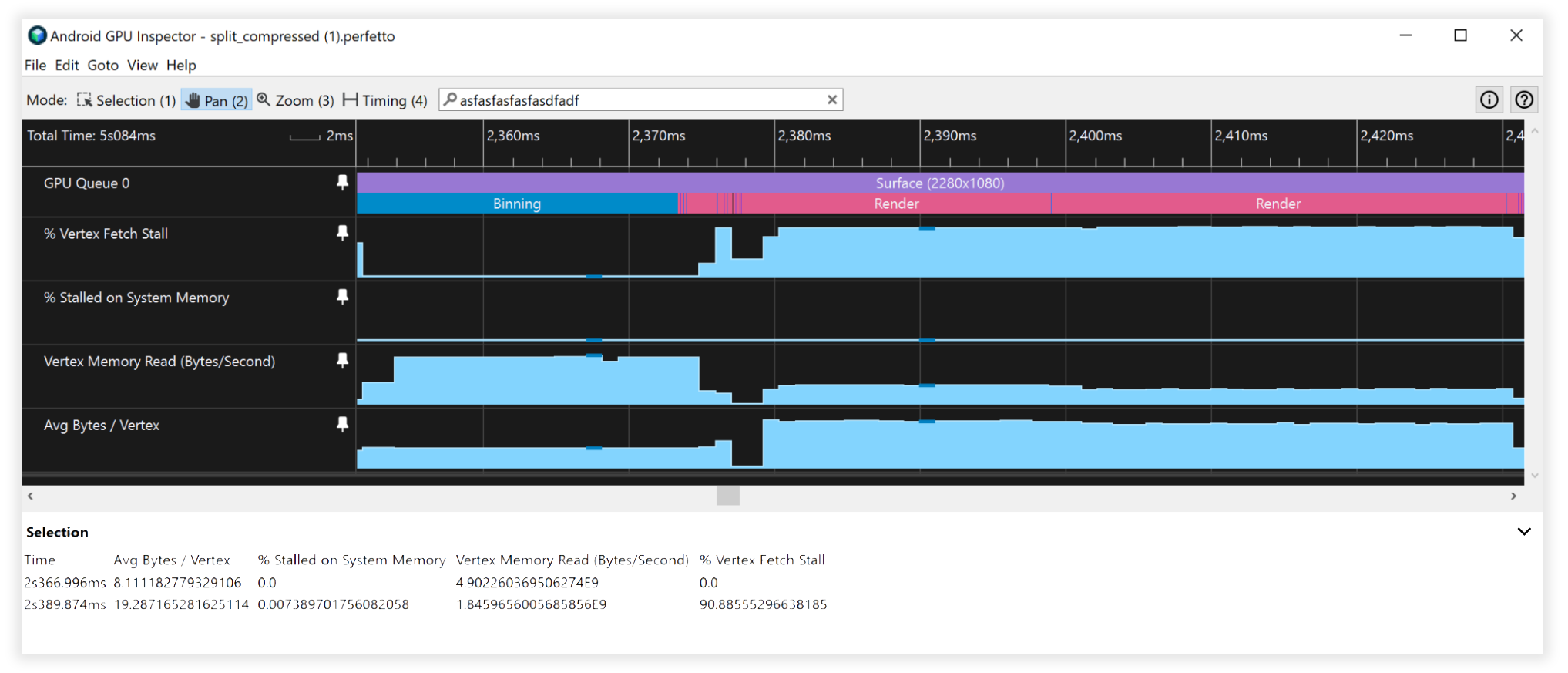
Ilustracja 8. Widok Inspektora GPU na Androidzie:podzielone, skompresowane strumienie wierzchołków

Inne rzeczy, które warto wziąć pod uwagę

16-bitowe a 32-bitowe dane bufora indeksu

• Zawsze dziel lub dziel siatki, tak aby zmieściły się w 16-bitowym buforze indeksu (maksymalnie 65 536 unikalnych wierzchołków). Pomoże to w renderowaniu indeksowanym na urządzeniach mobilnych, ponieważ pobieranie danych wierzchołków będzie tańsze i zużywa mniej energii.

Nieobsługiwane formaty atrybutów Vertex Buffer

• Formaty wierzchołków SSCALED nie są powszechnie obsługiwane na urządzeniach mobilnych, a ich używanie może powodować kosztowny spadek wydajności u sterowników usiłujących je emulować w przypadku braku obsługi sprzętowej. Postaw na SNORM i płać z drugiej strony ALU na dekompresję.