Une bonne mise en page et compression des données de sommet sont essentielles aux performances de toute application graphique, qu'elle implique des interfaces utilisateur 2D ou de grands jeux 3D en monde ouvert. Les tests internes effectués avec Frame Profiler d'Android GPU Inspector sur des dizaines de jeux Android parmi les plus populaires indiquent que la gestion des données de sommet mériterait d'être améliorée. Nous avons constaté que les données de sommet utilisent souvent une précision totale, des valeurs flottantes 32 bits pour tous les attributs de sommet et une mise en page de tampon de sommet qui repose sur un tableau de structures mises en forme avec des attributs entièrement entrelacés.
Cet article explique comment optimiser les performances graphiques de votre application Android à l'aide des techniques suivantes :
- Compression des sommets
- Fractionnement du flux de sommets
La mise en œuvre de ces techniques permet d'améliorer l'utilisation de la bande passante de la plate-forme de sommets (avec une amélioration pouvant atteindre 50 %), de réduire les conflits entre les bus de mémoire et le processeur, de limiter la charge de la mémoire système et d'accroître l'autonomie de la batterie. Et tous ces avantages bénéficient autant aux développeurs qu'aux utilisateurs finaux.
Toutes les données présentées proviennent d'un exemple de scène statique contenant environ 19 000 000 sommets exécutés sur un Pixel 4 :

Figure 1: Exemple de scène avec 6 anneaux et 19 millions de sommets
Compression des sommets
La compression des sommets est un terme générique qui désigne les techniques de compression avec pertes qui utilisent un empaquetage efficace pour réduire la taille des données de sommet pendant l'exécution et le stockage. La compression de la taille des sommets présente plusieurs avantages, notamment la réduction de la bande passante mémoire sur le GPU (en échangeant le calcul contre la bande passante), l'amélioration de l'utilisation du cache et la restriction potentielle du risque de débordement des registres.
Voici quelques approches courantes de la compression des sommets :
- Réduction de la précision numérique des attributs de données de sommet (par exemple, conversion d'un float 32 bits en float 16 bits)
- Représentation des attributs dans différents formats
Par exemple, si un sommet utilise des floats 32 bits complets pour la position (vec3), les coordonnées normales (vec3) et les coordonnées de texture (vec2), le remplacement de tous ces éléments par des floats 16 bits réduira la taille du sommet de 50 % (16 octets pour un sommet moyen de 32 octets).
Positions des sommets
Dans la grande majorité des maillages, les données de position des sommets peuvent faire l'objet d'une compression des valeurs à virgule flottante 32 bits de haute précision en valeurs à virgule flottante 16 bits de demi-précision. Les valeurs de demi-précision sont compatibles avec presque tous les appareils mobiles. Une fonction de conversion d'une valeur float32 en valeur float16 ressemble à ce qui suit (adaptée à partir de ce guide) :
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
Cette approche présente des limites : la précision se dégrade à mesure que le sommet s'éloigne de l'origine, ce qui le rend moins adapté aux maillages très volumineux dans l'espace (sommets dont les éléments dépassent 1 024 pixels). Pour résoudre ce problème, divisez le maillage en segments plus petits. Centrez chaque fragment autour de l'origine du modèle et effectuez une mise à l'échelle de sorte que tous les sommets de chaque fragment correspondent à la plage [-1, 1], qui contient la plus haute précision pour les valeurs à virgule flottante. Le pseudo-code de compression se présente comme suit :
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
Vous incorporerez le facteur de scaling et la translation dans la matrice de modèles afin de décompresser les données de sommet lors du rendu. N'oubliez pas qu'il n'est pas conseillé d'utiliser cette même matrice de modèles pour transformer les normales, car une autre compression leur a été appliquée. Vous avez besoin d'une matrice sans ces transformations de décompression pour les normales. Vous pouvez également utiliser la matrice du modèle de base (qui est compatible avec les normales), puis appliquer les transformations de décompression supplémentaires à la matrice du modèle dans le nuanceur. Exemple :
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
Une autre approche consiste à recourir à des entiers normalisés signés (également appelés SNORM). Les types de données SNORM utilisent des entiers plutôt que des valeurs à virgule flottante pour représenter les valeurs comprises entre [-1 et 1]. L'utilisation d'une norme SNORM 16 bits pour les positions vous permet de réaliser les mêmes économies de mémoire qu'une valeur float16 sans avoir à subir les inconvénients des distributions non uniformes. Une implémentation que nous recommandons d'utiliser avec SNORM se présente comme suit :
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| Format | Taille | |
|---|---|---|
| Avant | vec4<float32> |
16 octets |
| Après | vec3<float16/SNORM16> |
6 octets |
Normales aux sommets et espace tangent
Les normales aux sommets sont nécessaires pour la luminosité, tandis que l'espace tangent est nécessaire pour des techniques plus complexes telles que le mappage des normales.
Espace tangent
L'espace tangent est un système de coordonnées où chaque sommet est constitué du vecteur normal, tangent et bitangent. Comme ces trois vecteurs sont généralement orthogonaux les uns par rapport aux autres, il suffit de n'en stocker que deux pour pouvoir calculer le troisième en effectuant un croisement des deux premiers vecteurs dans le nuanceur de sommet.
Ces vecteurs peuvent généralement être représentés par des floats 16 bits sans perte perceptuelle de la fidélité visuelle. C'est donc un bon point de départ.
Nous pouvons aller encore plus loin dans la compression à l'aide d'une technique connue sous le nom de QTangents, qui stocke l'intégralité de l'espace tangent dans un seul quaternion. Les quaternions peuvent être utilisés pour représenter des rotations. Par conséquent, en considérant les vecteurs d'espace tangent comme des vecteurs colonnes d'une matrice 3x3 représentant une rotation (dans ce cas, de l'espace modèle à l'espace tangent), la conversion entre les deux est possible. Un quaternion peut être traité comme vec4 du point de vue des données. La conversion des vecteurs de l'espace tangent en QTangent conformément à l'article dont le lien est indiqué ci-dessus (et adaptée à partir de cette implémentation) se présente comme suit :
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
Le quaternion sera normalisé. Vous pourrez donc le compresser à l'aide de SNORM. Les SNORM 16 bits permettent d'économiser de la mémoire et offrent un bon niveau de précision. Les SNORM 8 bits contribuent à vous faire réaliser encore plus d'économies, mais peuvent générer des artefacts sur des matériaux très spécifiques. Vous pouvez tester les deux et déterminer ce qui fonctionne le mieux pour vos éléments. L'encodage du quaternion se présente comme suit :
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
Voici comment décoder le quaternion dans le nuanceur de sommets (adapté à partir d'ici) :
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| Format | Taille | |
|---|---|---|
| Avant | vec3<float32> + vec3<float32> + vec3<float32> |
36 octets |
| Après | vec4<SNORM16> |
8 octets |
Normales uniquement
Si vous n'avez besoin de stocker que des vecteurs de normales, vous pouvez réaliser davantage d'économies en utilisant le mappage octaédrique des vecteurs unitaires et non des coordonnées cartésiennes pour compresser le vecteur de normale. Le mappage octaédrique consiste à projeter une sphère unitaire en octaèdre, puis à projeter cet octaèdre en plan bidimensionnel. Vous pouvez donc représenter n'importe quel vecteur de normale à l'aide de deux nombres uniquement. Ces deux nombres peuvent être considérés comme des coordonnées de texture que nous utilisons pour "échantillonner" le plan bidimensionnel sur lequel nous avons projeté la sphère, ce qui nous permet de récupérer le vecteur d'origine. Ils peuvent ensuite être stockés dans une norme SNORM8.

Figure 2: Visualisation du mappage octaédrique (source)
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
La décompression dans le nuanceur de sommets (pour effectuer la reconversion en coordonnées cartésiennes) est peu coûteuse. Avec la plupart des appareils mobiles modernes, nous n'avons constaté aucune dégradation importante des performances lors de l'implémentation de cette technique. Décompression dans le nuanceur de sommets :
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
Cette approche permet également de stocker l'intégralité de l'espace tangent. Vous pouvez ainsi stocker le vecteur de normale et le vecteur de tangente à l'aide de vec2<SNORM8>, mais vous devrez trouver un moyen de stocker la direction de la bitangente (nécessaire pour le scénario courant où les coordonnées UV sont mises en miroir sur un modèle). Pour ce faire, vous pouvez mapper un composant de l'encodage du vecteur de la tangente pour qu'il soit toujours positif, puis inverser son signe si vous devez inverser la direction de la bitangente et effectuer les vérifications nécessaires dans le nuanceur de sommets :
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| Format | Taille | |
|---|---|---|
| Avant | vec3<float32> |
12 octets |
| Après | vec2<SNORM8> |
2 octets |
Coordonnées UV des sommets
Les coordonnées UV (utilisées pour le mappage des textures, entre autres) sont généralement stockées à l'aide de floats 32 bits. Si vous les compressez avec des floats 16 bits, vous risquez de rencontrer des problèmes de précision pour les textures supérieures à 1 024 x 1 024. La précision en virgule flottante entre [0,5, 1,0] signifie que les valeurs seront incrémentées de plus de 1 pixel.
L'approche la plus adaptée consiste à utiliser des entiers normalisés non signés (UNORM), en particulier UNORM16. Vous bénéficiez ainsi d'une répartition uniforme sur toute la plage de coordonnées pour des textures pouvant atteindre 65 536 x 65 536. Les coordonnées des textures doivent se situer dans la plage [0,0, 1,0] par élément, ce qui n'est pas toujours le cas en fonction du maillage (par exemple, les murs peuvent utiliser des coordonnées de texture qui vont au-delà de 1). Il est donc important de tenir compte de ce détail lorsque vous envisagez cette technique. La fonction de conversion se présente comme suit :
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| Format | Taille | |
|---|---|---|
| Avant | vec2<float32> |
8 octets |
| Après | vec2<UNORM16> |
4 octets |
Résultats de la compression des sommets
Ces techniques de compression des sommets ont permis de réduire de 66 % le stockage en mémoire des sommets, en passant de 48 octets à 16 octets. Voici les autres conséquences de cette compression :
- Bande passante de lecture de la mémoire des sommets :
- Binning : de 27 Go/s à 9 Go/s
- Rendu : de 4,5 à 1,5 Go/s
- Décrochage de la récupération des sommets :
- Binning : de 50 % à 0 %
- Rendu : de 90 % à 90 %
- Nombre moyen d'octets par sommet :
- Binning : de 48 à 16 milliards
- Rendu : de 52 à 18 milliards
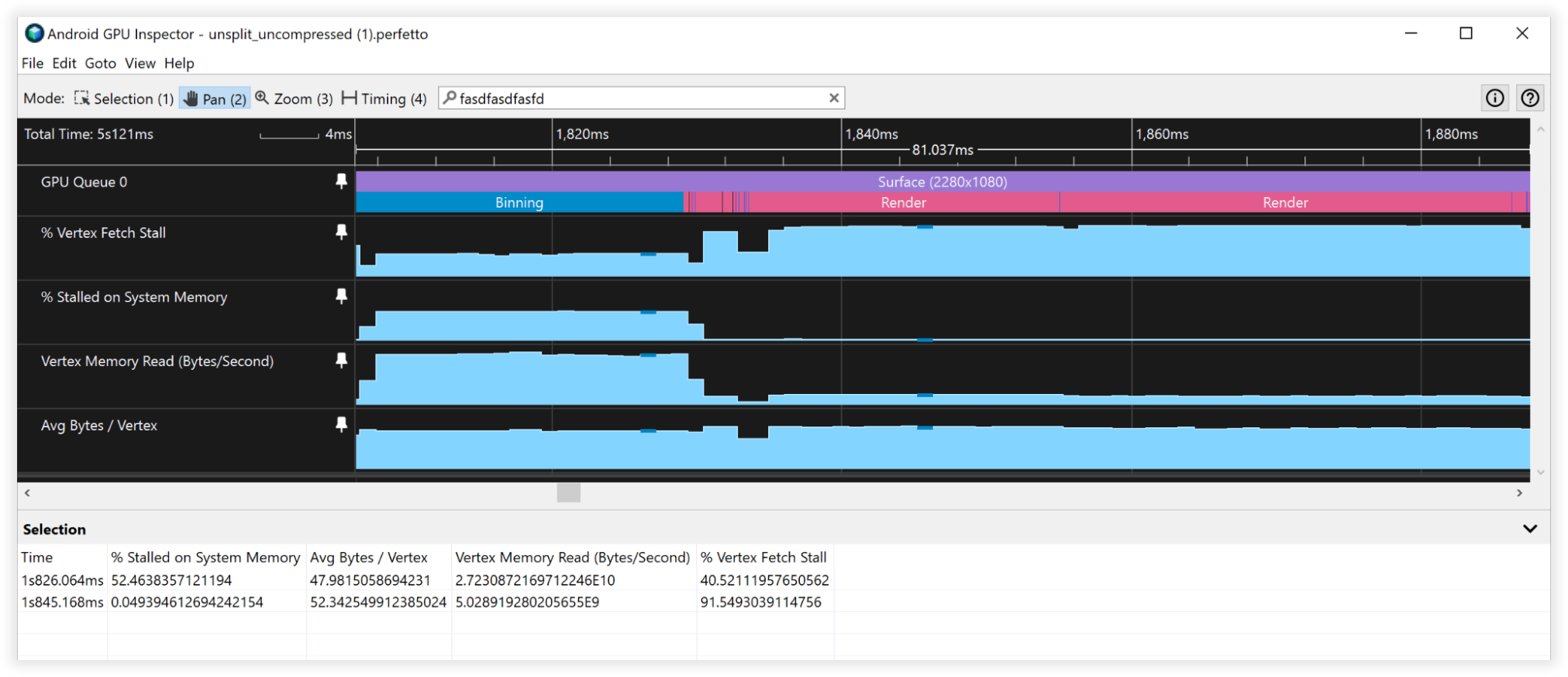
Figure 3: Vue des sommets non compressés dans Android GPU Inspector
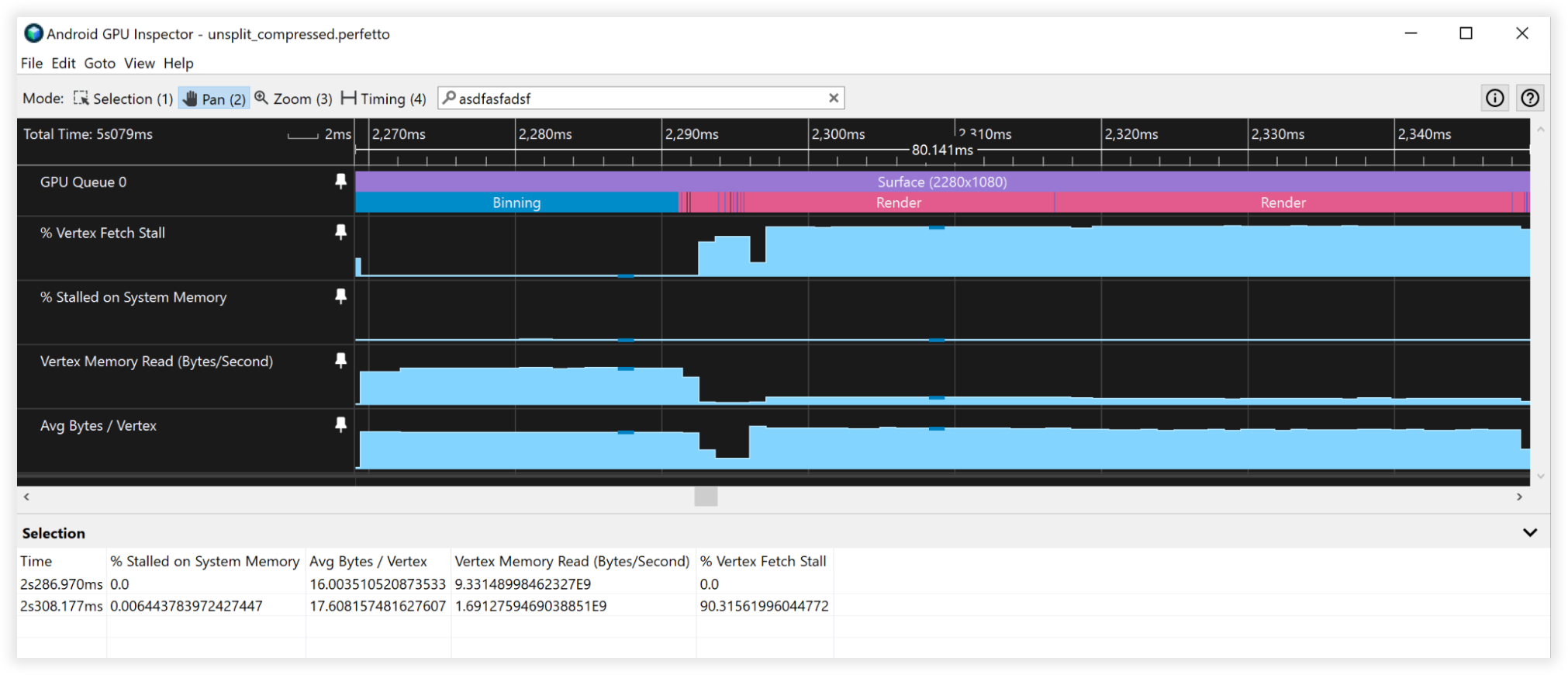
Figure 4: Vue des sommets compressés dans Android GPU Inspector
Fractionnement du flux de sommets
Le fractionnement du flux de sommets optimise l'organisation des données dans le tampon des sommets. Cette optimisation des performances du cache fait la différence sur les GPU basés sur des tuiles, généralement utilisés sur les appareils Android, en particulier au cours de l'étape de binning du processus de rendu.
Ces GPU créent un nuanceur qui calcule les coordonnées normalisées de l'appareil en fonction du nuanceur de sommets fourni pour effectuer le binning. Il est exécuté en premier sur chaque sommet de la scène, qu'il soit visible ou non. C'est pourquoi il est important que les données de position des sommets restent contiguës en mémoire. Cette répartition de flux de sommets peut également s'avérer utile pour les passes d'ombre, car vous n'avez généralement besoin que de données de position pour les calculs d'ombres et de prépasses de profondeur. Il s'agit d'une technique généralement utilisée pour le rendu sur console ou sur ordinateur. Cette mise en page du flux des sommets peut être utile pour plusieurs classes du moteur de rendu.
Le fractionnement du flux implique la configuration du tampon de sommet avec une section contiguë de données de position de sommet et une autre section contenant les attributs de sommet entrelacés. La plupart des applications configurent généralement leurs tampons de façon à entrelacer tous les attributs. Ce visuel explique cette différence :
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
Examiner la manière dont le GPU récupère les données de sommet nous aide à comprendre les avantages du fractionnement de flux. Pour les besoins de cet argument, supposons que nous utilisons les valeurs suivantes :
- Lignes de cache de 32 octets (taille assez courante)
- Format de sommet :
- Position, vec3<float32> = 12 octets
- Normale, vec3<float32> = 12 octets
- Coordonnées UV, vec2<float32> = 8 octets
- Taille totale = 32 octets
Lorsque le GPU extrait des données de la mémoire pour le binning, il extrait une ligne de cache de 32 octets. Sans le fractionnement du flux de sommets, seuls les 12 premiers octets de cette ligne de cache sont utilisés pour le binning, et les 20 autres octets sont supprimés lors de la récupération du sommet suivant. Avec le fractionnement du flux de sommets, les positions des sommets sont contiguës en mémoire. Par conséquent, lorsque ce fragment de 32 octets est mis en cache, il contient en réalité deux positions de sommet entières exploitables avant d'avoir à retourner dans la mémoire principale pour en extraire d'autres. Le nombre de positions de sommet disponibles est donc multiplié par deux.
Si nous combinons le fractionnement du flux de sommets avec la compression de sommets, nous réduisons la taille d'une seule position de sommet à 6 octets. Par conséquent, une seule ligne de cache de 32 octets extraite de la mémoire système dispose de cinq positions de sommet entier, soit cinq fois plus.
Résultats du fractionnement du flux de sommets
- Bande passante de lecture de la mémoire des sommets :
- Binning : de 27 Go/s à 6,5 Go/s
- Rendu : de 4,5 Go/s à 4,5 Go/s
- Décrochage de la récupération des sommets :
- Binning : de 40 % à 0 %
- Rendu : de 90 % à 90 %
- Nombre moyen d'octets par sommet :
- Binning : de 48 à 12 milliards
- Rendu : de 52 à 52 milliards

Figure 5: Vue des flux de sommets non fractionnés dans Android GPU Inspector
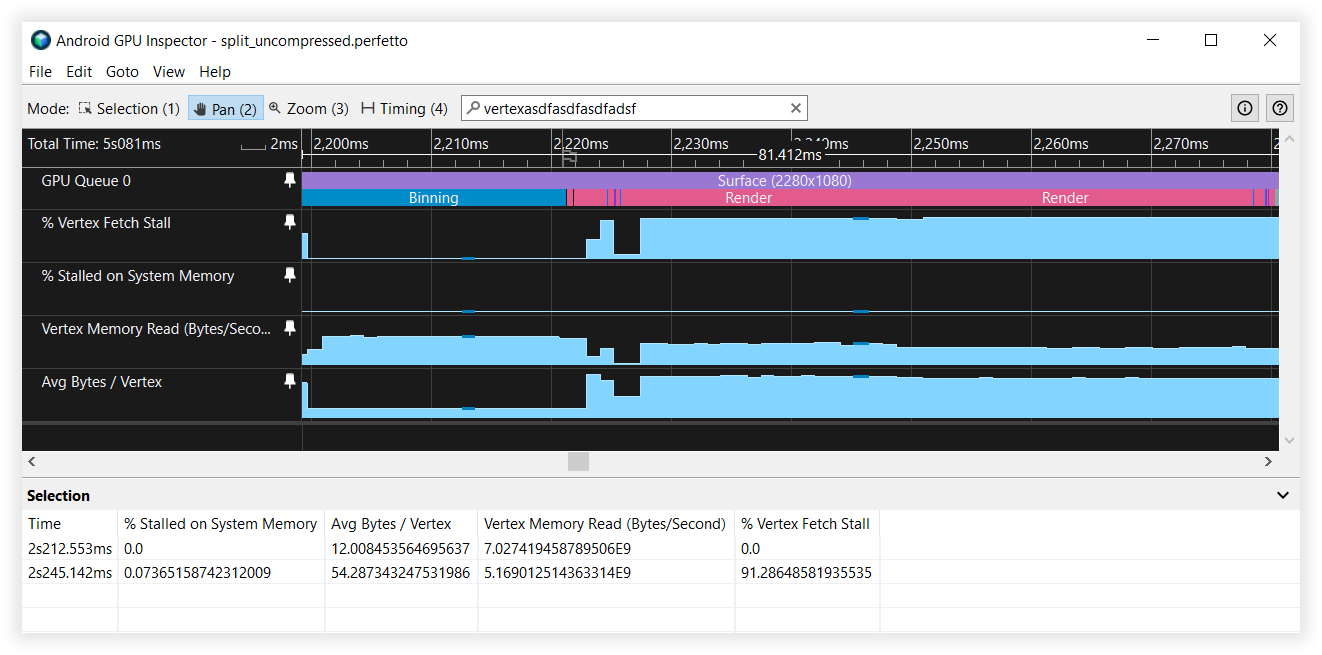
Figure 6: Vue des flux de sommets fractionnés dans Android GPU Inspector
Résultats composés
- Bande passante de lecture de la mémoire des sommets :
- Binning : de 25 Go/s à 4,5 Go/s
- Rendu : de 4,5 Go/s à 1,7 Go/s
- Décrochage de la récupération des sommets :
- Binning : de 41 % à 0 %
- Rendu : de 90 % à 90 %
- Nombre moyen d'octets par sommet :
- Binning : de 48 à 8 milliards
- Rendu : de 52 à 19 milliards

Figure 7: Vue des flux de sommets non compressés et non fractionnés dans Android GPU Inspector
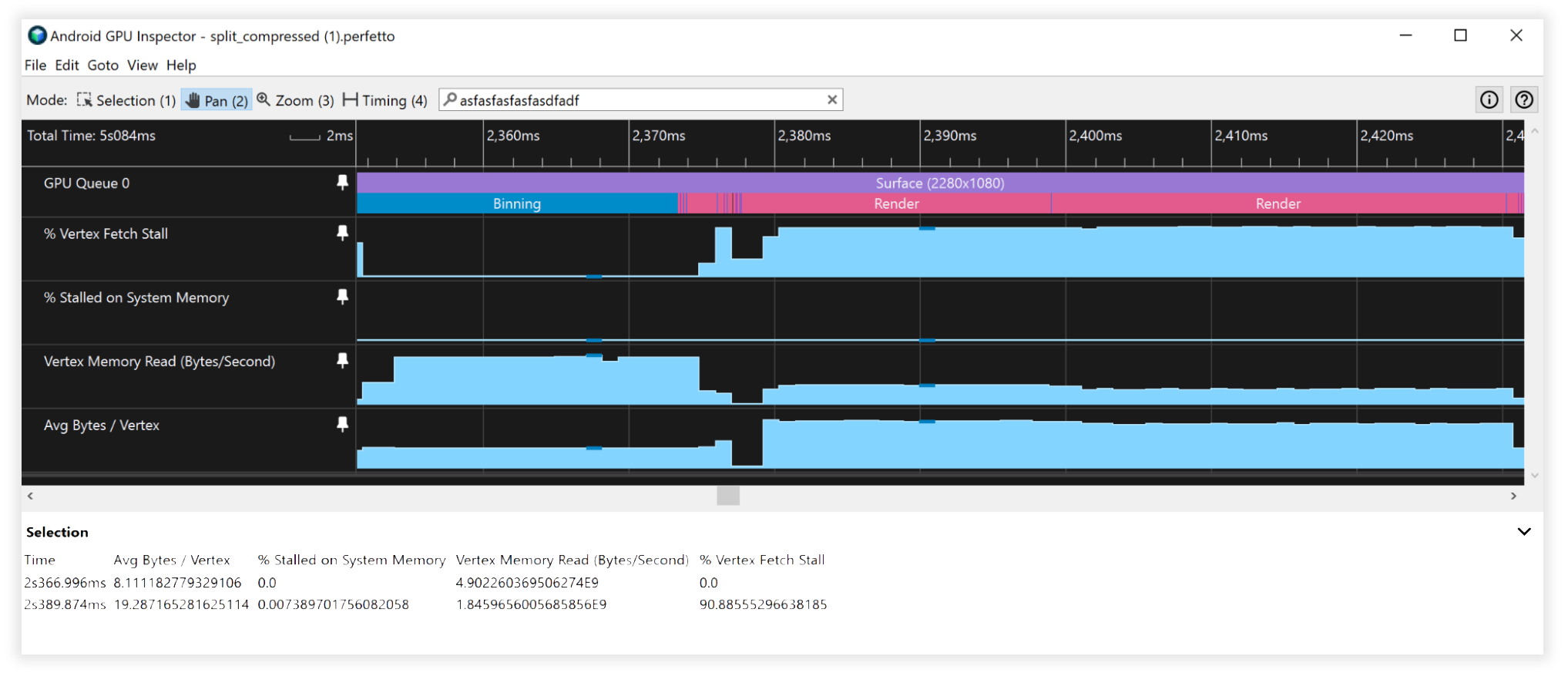
Figure 8: Vue des flux de sommets compressés et fractionnés dans Android GPU Inspector
Facteurs supplémentaires
Données de tampon d'index 16 bits ou 32 bits
- Fractionnez toujours les maillages de sorte qu'ils rentrent dans un tampon d'index 16 bits (65 536 sommets uniques maximum). Cette approche favorise le rendu indexé sur mobile, car il est moins coûteux d'extraire des données de sommet et que la consommation d'énergie est moindre.
Formats d'attribut de tampon de sommets non compatibles
- Les formats de sommet SSCALED ne sont pas compatibles avec les appareils mobiles. Lorsqu'ils sont utilisés, ils peuvent impliquer des compromis coûteux en termes de performances dans les pilotes qui tentent de les émuler si le matériel sous-jacent ne les prend pas en charge. Mieux vaut opter pour SNORM et payer le coût ALU négligeable pour la décompression.
