Administración de datos de Vertex

Un buen diseño y compresión de datos de vértices es fundamental para el rendimiento de cualquier aplicación gráfica, ya sea que esta consista en interfaces de usuario en 2D o sea un gran juego de mundo abierto en 3D. Las pruebas internas con el Generador de perfiles del Inspector de GPU de Android en decenas de juegos principales de Android indican que se puede hacer mucho para mejorar la administración de datos de vértices. Notamos que es común que los datos de vértices usen valores flotantes de 32 bits de precisión completa en todos sus atributos, así como un diseño de búfer de vértices que usa un array de estructuras con atributos completamente intercalados.

En este artículo, se aborda la manera de optimizar el rendimiento de los gráficos de tu aplicación para Android mediante las siguientes técnicas:

• Compresión de Vertex
• División de la transmisión de Vertex

Implementar estas técnicas puede mejorar el uso del ancho de banda de memoria de vértices en hasta un 50%, reducir la contención del bus de memoria con la CPU, reducir los bloqueos en la memoria del sistema y mejorar la duración de batería, lo cual resulta beneficioso tanto para los desarrolladores como para los usuarios finales.

Todos los datos presentados provienen de una escena estática de ejemplo que contiene alrededor de 19,000,000 de vértices que se ejecutan en un Pixel 4:

Figura 1: Escena de muestra con 6 anillos y 19 millones de vértices

Compresión de Vertex

La compresión de Vertex es un término amplio utilizado para técnicas de compresión con pérdida que usan paquetes eficientes a fin de reducir el tamaño de los datos de vértices tanto en el tiempo de ejecución como en el almacenamiento. Disminuir el tamaño de los vértices tiene varios beneficios, como la reducción del ancho de banda de memoria en la GPU (mediante el intercambio de procesamiento por ancho de banda), la mejora del uso de la caché y la posible reducción del riesgo de desborde de registros.

Los siguientes son algunos de los enfoques comunes de la compresión de Vertex:

• Reducir la precisión numérica de los atributos de datos de vértices (p. ej.: flotante de 32 bits a flotante de 16 bits)
• Representar los atributos en formatos diferentes

Por ejemplo, si un vértice usa flotantes de precisión completa de 32 bits para la posición (vec3), la normal (vec3) y la coordenada de textura (vec2), cuando se reemplacen todos estos con flotantes de 16 bits, se reducirá el tamaño del vértice en un 50% (16 bytes en un vértice normal de 32 bytes).

Posiciones de vértice

En la gran mayoría de las mallas, los datos de posición de vértices se pueden comprimir de valores de punto flotante de 32 bits de precisión completa a unos de 16 bits de precisión media, los cuales son compatibles en el hardware de casi todos los dispositivos móviles. Una función de conversión que va de float32 a float16 se ve de la siguiente manera (adaptada de esta guía):

uint16_t f32_to_f16(float f) {
  uint32_t x = (uint32_t)f;
  uint32_t sign = (unsigned short)(x >> 31);
  uint32_t mantissa;
  uint32_t exp;
  uint16_t hf;

  mantissa = x & ((1 << 23) - 1);
  exp = x & (0xFF << 23);
  if (exp >= 0x47800000) {
    // check if the original number is a NaN
    if (mantissa && (exp == (0xFF << 23))) {
      // single precision NaN
      mantissa = (1 << 23) - 1;
    } else {
      // half-float will be Inf
      mantissa = 0;
    }
    hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
         (uint16_t)(mantissa >> 13);
  }
  // check if exponent is <= -15
  else if (exp <= 0x38000000) {
    hf = 0;  // too small to be represented
  } else {
    hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
         (uint16_t)(mantissa >> 13);
  }

  return hf;
}

Este enfoque tiene una limitación: la precisión se degrada a medida que el vértice se aleja del origen, lo cual lo hace menos adecuado para las mallas que son demasiado grandes desde el punto de vista espacial (vértices con elementos que superan los 1,024). Puedes solucionar esto dividiendo una malla en fragmentos más pequeños, centrando cada uno en el origen del modelo y ajustando la escala de modo que todos sus vértices se ajusten al rango [-1, 1], que contiene la mayor precisión para los valores de punto flotante. El pseudocódigo de la compresión tiene el siguiente aspecto:

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));

Prepara el factor de escala y la traslación en la matriz del modelo a fin de descomprimir los datos de vértices durante la renderización. Ten en cuenta que no es bueno usar esta misma matriz para transformar normales, ya que no tienen aplicada la misma compresión. Necesitarás una matriz sin estas transformaciones de descompresión para normales o puedes usar la matriz del modelo base (que sí puedes usar para las normales) y, luego, aplicar las transformaciones adicionales de descompresión a la matriz del modelo dentro del sombreador. Por ejemplo:

vec3 in in_pos;

void main() {
   ...
   // bounding box data packed into uniform buffer
   vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
   gl_Position = proj * view * model * decompress_pos;
}

Otro enfoque consiste en usar números enteros normalizados con signo (SNORM). Los tipos de datos SNORM usan números enteros en lugar de un punto flotante a efectos de representar valores en el rango [-1, 1]. El uso de un SNORM de 16 bits para posiciones brinda el mismo ahorro de memoria que un float16, sin las desventajas de las distribuciones no uniformes. Una implementación que recomendamos para el uso de SNORM se ve de la siguiente manera:

const int BITS = 16

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   // float to integer value conversion
   p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1) 

	Formato	Tamaño
Antes	vec4<float32>	16 bytes
Después	vec3<float16/SNORM16>	6 bytes

Espacio tangente y normales de un vértice

Las normales de un vértice se utilizan para la iluminación, mientras que el espacio tangente se necesita para técnicas más complejas, como el mapeo de normales.

Espacio tangente

El espacio tangente es un sistema de coordenadas en el que cada vértice consta de los vectores normal, tangente y bitangente. Debido a que estos tres vectores suelen ser ortogonales entre sí, solo tendremos que almacenar dos: podemos calcular el tercero realizando el producto cruzado de los otros dos en el sombreador del vértice.

Por lo general, estos vectores se pueden representar con flotantes de 16 bits sin ninguna pérdida perceptiva de fidelidad visual; por lo tanto, son un buen punto de partida.

Podemos realizar una compresión aún mayor mediante una técnica conocida como QTangents, que almacena todo el espacio tangente en un solo cuaternión. Dado que se pueden usar cuaterniones a fin de representar rotaciones, si pensamos en los vectores del espacio tangente como vectores columna de una matriz de 3x3 que representa una rotación (en este caso, del espacio del modelo al espacio tangente), podremos realizar la conversión entre ambos. En términos de datos, un cuaternión se puede tratar como vec4. A continuación, se muestra una conversión de vectores del espacio tangente a un QTangent con base en el informe vinculado anteriormente y adaptado a partir de la presente implementación:

const int BITS = 16

quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
   mat3 tbn = {normal, tangent, bitangent};
   quaternion qTangent(tbn);
   qTangent.normalize();

   //Make sure QTangent is always positive
   if (qTangent.w < 0)
       qTangent = -qTangent;

   const float bias = 1.0 / (2^(BITS - 1) - 1);

   //Because '-0' sign information is lost when using integers,
   //we need to apply a "bias"; while making sure the Quaternion
   //stays normalized.
   // ** Also our shaders assume qTangent.w is never 0. **
   if (qTangent.w < bias) {
       Real normFactor = Math::Sqrt( 1 - bias * bias );
       qTangent.w = bias;
       qTangent.x *= normFactor;
       qTangent.y *= normFactor;
       qTangent.z *= normFactor;
   }

   //If it's reflected, then make sure .w is negative.
   vec3 naturalBinormal = cross_product(tangent, normal);
   if (dot_product(naturalBinormal, binormal) <= 0)
       qTangent = -qTangent;
   return qTangent;
}

Se normalizará el cuaternión y podrás comprimirlo usando SNORM. Los SNORM de 16 bits brindan una precisión y un ahorro de memoria adecuados. Los SNORM de 8 bits pueden generar un ahorro mayor, pero podrían provocar desperfectos en materiales muy especulares. Puedes probar ambos y ver cuál funciona mejor con tus elementos. La codificación del cuaternión tiene el siguiente aspecto:

for each vertex v in mesh:
   quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
   // Once we have the quaternion we can compress it
   res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);

A continuación, se incluye la decodificación del cuaternión en el sombreador de vértices (adaptado desde aquí):

vec3 xAxis( vec4 qQuat )
{
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwy = fTy * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxy = fTy * qQuat.x;
  float fTxz = fTz * qQuat.x;
  float fTyy = fTy * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}

vec3 yAxis( vec4 qQuat )
{
  float fTx  = 2.0 * qQuat.x;
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwx = fTx * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxx = fTx * qQuat.x;
  float fTxy = fTy * qQuat.x;
  float fTyz = fTz * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}

void main() {
  vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
  vec3 normal = xAxis(qtangent);
  vec3 tangent = yAxis(qtangent);
  float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
  vec3 binormal = cross(normal, tangent) * biNormalReflection;
  ...
}

	Formato	Tamaño
Antes	vec3<float32> y vec3<float32> y vec3<float32>	36 bytes
Después	vec4<SNORM16>	8 bytes

Solo vectores normales

Si solo necesitas almacenar vectores normales, existe un enfoque diferente que puede generar un mayor ahorro: se trata de usar el Mapeo octaédrico de vectores unitarios en lugar de las coordenadas cartesianas para comprimir el vector normal. El mapeo octaédrico funciona proyectando una esfera unitaria sobre un octaedro y, luego, proyectando este último sobre un plano en 2D. El resultado consiste en que podrás representar cualquier vector normal usando solo dos números. Estos dos números se pueden considerar como coordenadas de textura que usamos para "mostrar" el plano en 2D sobre el que proyectamos la esfera, lo que nos permite recuperar el vector original. Luego, dichos números se podrán almacenar en un SNORM8.

Figura 2: Mapeo octaédrico visualizado (fuente)

const int BITS = 8

// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
  float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
  vec2 res;
  if (n.z < 0.0) {
    res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
    res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
  } else {
    res.x = n.x * invL1Norm;
    res.y = n.y * invL1Norm;
  }
  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

La descompresión en el sombreador de vértices (para volver a las coordenadas cartesianas) tiene un costo bajo: en la mayoría de los dispositivos móviles modernos, cuando implementamos esta técnica, no observamos una degradación importante del rendimiento. La descompresión en el sombreador de vértices:

//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
  vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
  float t = max(-v.z, 0.0);
  v.xy += t * -sign(v.xy);
  return v;

También se puede usar este enfoque a fin de almacenar todo el espacio tangente utilizando esta técnica para almacenar los vectores normal y tangente con vec2<SNORM8>, pero necesitarás encontrar una manera de almacenar la dirección del vector bitangente (resulta necesario cuando hayas duplicado las coordenadas UV en un modelo, lo cual es una situación habitual). Una forma de implementar esto es mapear un componente de tu vector tangente, codificarlo de modo que siempre sea positivo, cambiarle el signo en caso de que necesites invertir la dirección de la bitangente y comprobar si lo ves en el sombreador de vértices:

const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)

// Compressing
for each normal n in mesh:
  //encode to octahedron, result in range [-1, 1]
  vec2 res = vec_to_oct(n);

  // map y to always be positive
  res.y = res.y * 0.5 + 0.5;

  // add a bias so that y is never 0 (sign in the vertex shader)
  if (res.y < bias)
    res.y = bias;

  // Apply the sign of the binormal to y, which was computed elsewhere
  if (binormal_sign < 0)
    res.y *= -1;

  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);

	Formato	Tamaño
Antes	vec3<float32>	12 bytes
Después	vec2<SNORM8>	2 bytes

Coordenadas UV del vértice

Las coordenadas UV, que se utilizan para mapear texturas (entre otras cosas), generalmente se almacenan con flotantes de 32 bits. Comprimirlas con flotantes de 16 bits generará problemas de precisión en texturas de más de 1,024 x 1,024. La precisión de punto flotante en el rango [0.5, 1.0] significa que los valores tendrán un incremento de más de 1 píxel.

El mejor enfoque es utilizar números enteros normalizados sin signo (UNORM), en particular, UNORM16, el cual proporciona una distribución uniforme en todo el rango de coordenadas de texturas y admite texturas de hasta 65,536 x 65,536. Esto supone que las coordenadas de texturas están dentro del rango [0.0, 1.0] por elemento, aunque este podría no ser el caso según la malla (por ejemplo, las paredes pueden usar coordenadas de texturas envolventes de más de 1.0). Ten esto en cuenta cuando evalúes esta técnica. La función de conversión tendrá el siguiente aspecto:

const int BITS = 16

for each vertex_uv V in mesh:
  V *= clamp(2^BITS - 1, 0, 2^BITS - 1);  // float to integer value conversion

	Formato	Tamaño
Antes	vec2<float32>	8 bytes
Después	vec2<UNORM16>	4 bytes

Resultados de la compresión de Vertex

Estas técnicas de compresión de vértices generaron una reducción del 66% en el almacenamiento de la memoria de vértices, que pasó de 48 bytes a 16 bytes. Esto se manifestó de la siguiente manera:

• Ancho de banda de lectura de memoria de Vertex:
  • Discretización: 27 GB/s a 9 GB/s
  • Renderización: 4.5 B/s a 1.5 GB/s
• Bloqueos de recuperación de Vertex:
  • Discretización: 50% a 0%
  • Renderización: 90% a 90%
• Promedio de bytes por vértice:
  • Discretización: 48 B a 16 B
  • Renderización: 52 B a 18 B

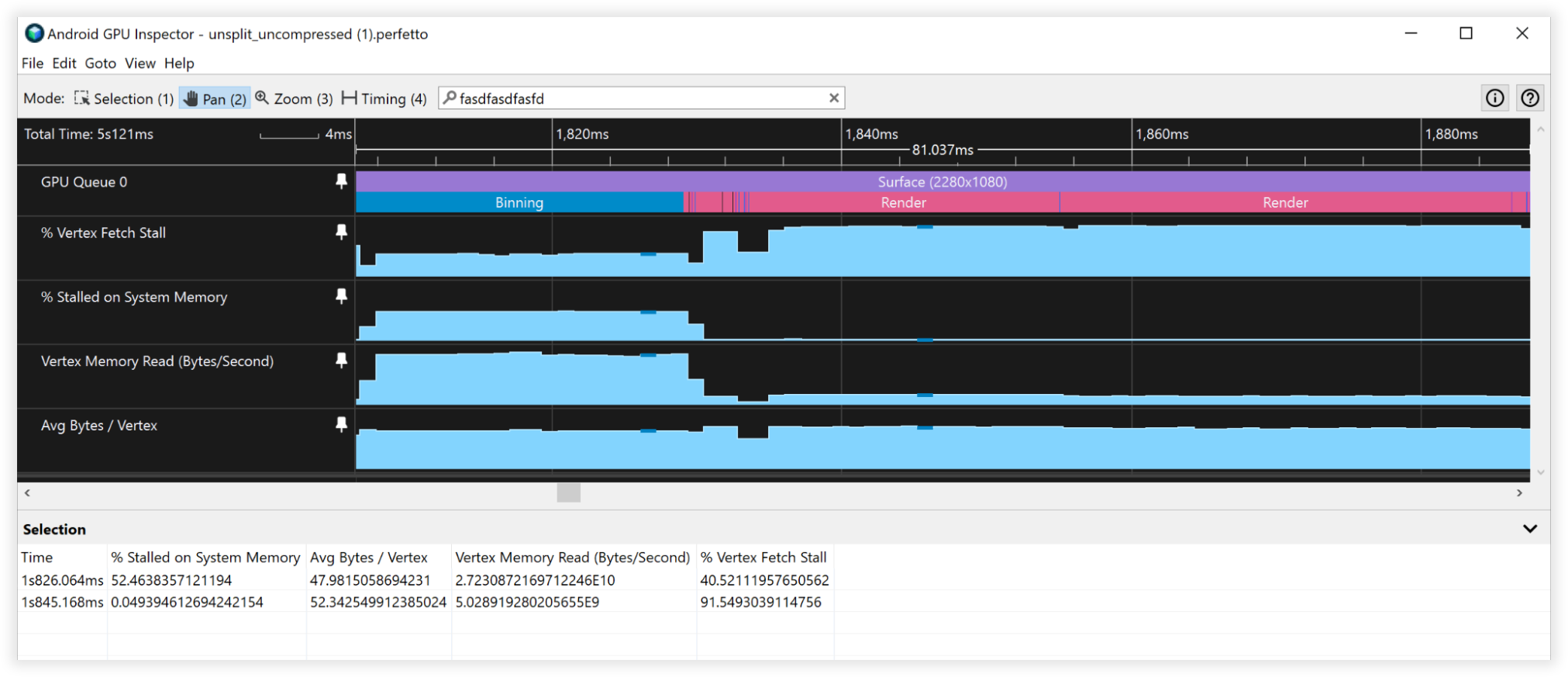
Figura 3: Vista de vértices sin comprimir del Inspector de GPU de Android

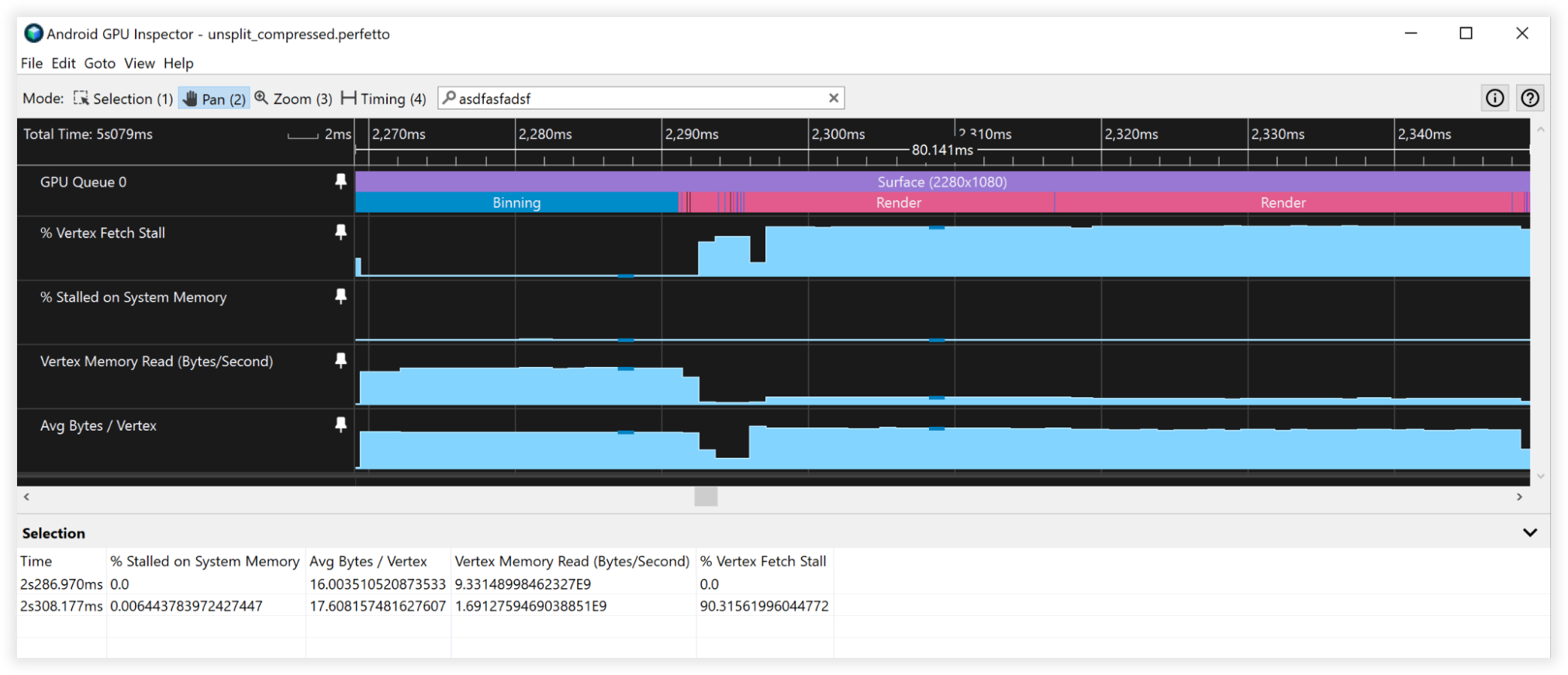
Figura 4: Vista de vértices comprimidos del Inspector de GPU de Android

División de la transmisión de Vertex

La división de la transmisión de Vertex optimiza la organización de los datos en el búfer de Vertex. Esta es una optimización del rendimiento de la caché que marca la diferencia en las GPU basadas en mosaicos que suelen encontrarse en los dispositivos Android, en particular durante el paso de discretización del proceso de renderización.

Las GPU basadas en mosaicos crean un sombreador que calcula las coordenadas normalizadas de los dispositivos en función del sombreador de vértices proporcionado a efectos de realizar la discretización. Se ejecuta primero en cada vértice de la escena, sea visible o no. Por lo tanto, es importante mantener contiguos los datos de posición de los vértices en la memoria. Otras instancias en las que este diseño de transmisión de vértices puede resultar provechoso es en los pases de las sombras (ya que, por lo general, solo necesitas datos de posición para realizar los cálculos de las sombras), así como en los pases previos de la profundidad (esta es una técnica que se suele usar para la renderización en consolas y computadoras de escritorio). Dicho diseño de transmisión de vértices puede ser beneficioso para varias clases del motor de renderización.

La división de la transmisión implica configurar el búfer de vértices con una sección contigua de datos de posición de vértices y otra sección que contenga atributos de vértices intercalados. Por lo general, la mayoría de las aplicaciones configuran sus búferes intercalando por completo todos los atributos. En el siguiente elemento visual, se explica la diferencia:

Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|

After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|

Ver cómo la GPU recupera los datos de vértices nos ayuda a comprender los beneficios de dividir la transmisión. Por poner un ejemplo, asumiremos lo siguiente:

• Líneas de caché de 32 bytes (un tamaño bastante común)
• Formato de vértice que consta de lo siguiente:
  • Posición vec3<float32> = 12 bytes
  • Normal vec3<float32> = 12 bytes
  • Coordenadas UV vec2<float32> = 8 bytes
  • Tamaño total = 32 bytes

Cuando la GPU recupere los datos de la memoria para la discretización, extraerá una línea de caché de 32 bytes a fin de realizar la operación. Sin la división de la transmisión de vértices, en realidad, solo se usarán los primeros 12 bytes de esta línea de caché a efectos de la discretización, y se descartarán los otros 20 bytes mientras se recupera el vértice siguiente. Con la división de la transmisión de vértices, las posiciones de los vértices estarán contiguas en la memoria, de modo que, cuando el fragmento de 32 bytes se extraiga a la caché, en realidad, contendrá 2 posiciones completas de vértices para realizar la operación antes de tener que volver a la memoria principal a fin de recuperar más, lo cual representa una mejora del 200%.

Ahora, si combinamos la división de la transmisión de vértices con la compresión de vértices, reduciremos el tamaño de una sola posición de vértice a 6 bytes, de modo que una sola línea de caché de 32 bytes extraída de la memoria del sistema tendrá 5 posiciones de vértice completas para operar, una mejora del 500%.

Resultados de la división de la transmisión de Vertex

• Ancho de banda de lectura de memoria de Vertex:
  • Discretización: 27 GB/s a 6.5 GB/s
  • Renderización: 4.5 GB/s a 4.5 GB/s
• Bloqueos de recuperación de Vertex:
  • Discretización: 40% a 0%
  • Renderización: 90% a 90%
• Promedio de bytes por vértice:
  • Discretización: 48 B a 12 B
  • Renderización: 52 B a 52 B

Figura 5: Vista de transmisiones de vértices sin dividir del Inspector de GPU de Android

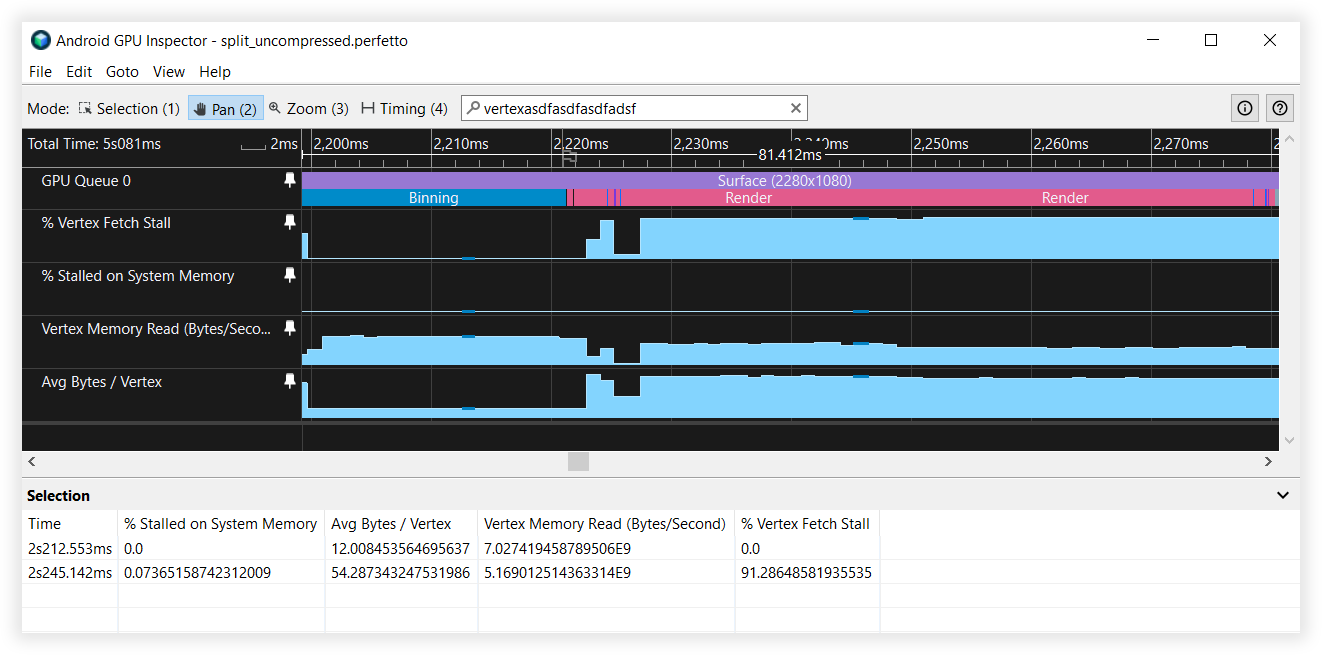
Figura 6: Vista de transmisiones de vértices divididos del Inspector de GPU de Android

Resultados compuestos

• Ancho de banda de lectura de memoria de Vertex:
  • Discretización: 25 GB/s a 4.5 GB/s
  • Renderización: 4.5 GB/s a 1.7 GB/s
• Bloqueos de recuperación de Vertex:
  • Discretización: 41% a 0%
  • Renderización: 90% a 90%
• Promedio de bytes por vértice:
  • Discretización: 48 B a 8 B
  • Renderización: 52 B a 19 B

Figura 7: Vista de transmisiones de vértices sin dividir ni comprimir del Inspector de GPU de Android

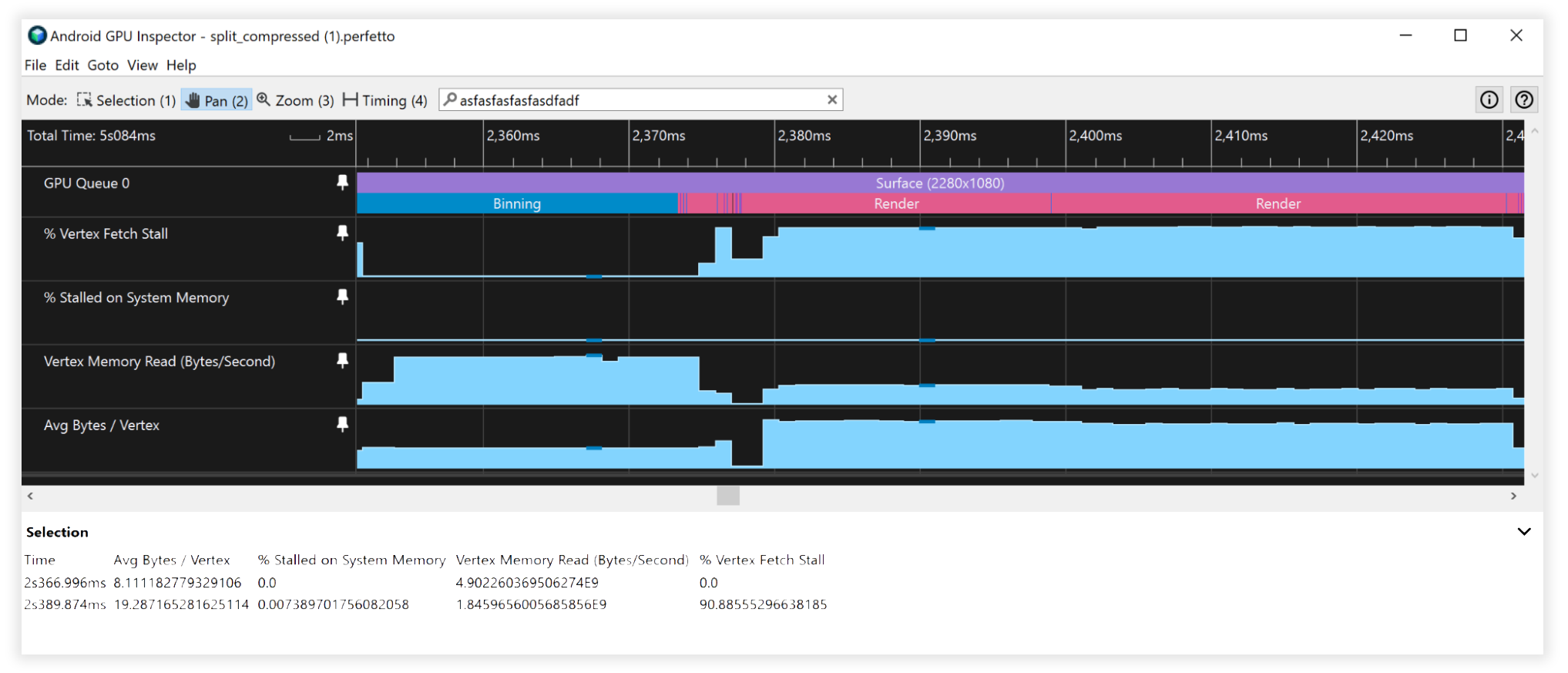
Figura 8: Vista de transmisiones de vértices comprimidos y divididos del Inspector de GPU de Android

Consideraciones adicionales

Comparación entre los datos de búfer de índice de 16 bits y 32 bits

• Siempre divide las mallas en fragmentos tales que se ajusten a un búfer de índice de 16 bits (como máximo, 65,536 vértices únicos). Esto ayudará con la renderización indexada en los dispositivos móviles, ya que resulta más económico recuperar datos de vértices y consumirá menos energía.

Formatos no admitidos de atributos de búfer de Vertex

• Los formatos de vértices SSCALED, por lo general, no son compatibles con dispositivos móviles y, cuando se usan, pueden tener desventajas relacionadas con un rendimiento costoso en los controladores que intenten emularlos si no son compatibles con el hardware. Siempre elige usar SNORM y paga el costo despreciable de ALU para realizar la descompresión.