Um bom layout e compactação de dados de vértice é essencial para o desempenho de qualquer aplicativo gráfico, independentemente de ser composto de interfaces de usuário 2D ou ser um jogo aberto em 3D. Testes internos com o Frame Profiler do Android GPU Inspector em dezenas dos principais jogos Android indicam que muito pode ser feito para melhorar o gerenciamento de dados de vértice. Percebemos que é comum que os dados de vértice usem precisão total, valores flutuantes de 32 bits para todos os atributos de vértice e um layout de buffer de vértice que usa uma matriz de estruturas formatadas com atributos totalmente intercalados.
Este artigo discute como otimizar o desempenho gráfico do seu app Android usando as seguintes técnicas:
- Compactação de vértices
- Divisão de fluxo de vértices
A implementação dessas técnicas pode melhorar o uso de largura de banda de memória de vértices em até 50%, reduzir a contenção de barramentos de memória com a CPU, reduzir interrupções de memória do sistema e melhorar a duração da bateria. Tudo isso é benéfico para desenvolvedores e usuários finais.
Todos os dados apresentados vêm de um exemplo de cena estática contendo aproximadamente 19 milhões de vértices em execução em um Pixel 4:

Figura 1: exemplo de cena com 6 anéis e vértices de 19 m
Compactação de vértices
A compactação de vértices é um termo abrangente para técnicas de compactação com perdas que usam empacotamento eficiente para reduzir o tamanho dos dados de vértices durante o tempo de execução e no armazenamento. A redução do tamanho dos vértices oferece diversos benefícios, incluindo a redução da largura de banda de memória na GPU (por meio da troca de computação por largura de banda), melhoria da utilização do cache e possível redução do risco de vazamentos de registros.
As abordagens mais comuns à compactação de vértices incluem:
- redução da precisão numérica dos atributos de dados de vértices (por exemplo, flutuante de 32 bits para flutuante de 16 bits),
- representação de atributos em diferentes formatos.
Por exemplo, se um vértice usa flutuantes de 32 bits completos para posição (vec3), normal (vec3) e coordenadas de textura (vec2), substituir todos eles por flutuantes de 16 bits reduz o tamanho do vértice em 50% (16 bytes em um vértice de 32 bytes em média).
Posições de vértices
Os dados de posição de vértices podem ser compactados de valores de ponto flutuante de 32 bits com precisão total para valores de ponto flutuante de 16 bits com meia precisão na grande maioria das malhas. Os flutuantes de meia precisão são compatíveis com o hardware em quase todos os dispositivos móveis. Uma função de conversão de float32 para float16 é semelhante a esta (adaptada deste guia em inglês):
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
Há uma limitação nessa abordagem. A precisão diminui conforme o vértice se afasta da origem, tornando-a menos adequada para malhas espacialmente muito grandes (vértices com elementos que ultrapassam 1.024). Você pode solucionar isso ao dividir uma malha em blocos menores, centralizando cada bloco em torno da origem do modelo e escalonando de modo que todos os vértices de cada bloco estejam dentro do intervalo [-1, 1], que contém a maior precisão para os valores de ponto flutuante. O pseudocódigo para compactação tem esta aparência:
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
Você incorpora o fator de escala e a conversão na matriz do modelo a fim de descompactar os dados de vértice ao renderizar. Lembre-se de que não convém usar essa mesma matriz de modelo para transformar os valores normais, já que eles não tiveram a mesma compactação aplicada. Você precisará de uma matriz sem essas transformações de descompactação para normais ou poderá usar a matriz de modelo base (que pode ser usada para normais) e aplicar as transformações de descompactação adicionais à matriz de modelo dentro do sombreador. Um exemplo:
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
Outra abordagem envolve o uso de números inteiros normalizados assinados (SNORM) (link em inglês). Os tipos de dados SNORM usam números inteiros em vez de ponto flutuante para representar valores entre [-1, 1]. O uso de um SNORM de 16 bits para posições oferece a mesma economia de memória que um float16, sem as desvantagens de distribuições não uniformes. Veja a seguir uma implementação que recomendamos para usar o SNORM:
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| Formato | Tamanho | |
|---|---|---|
| Antes | vec4<float32> |
16 bytes |
| Depois | vec3<float16/SNORM16> |
6 bytes |
Vértices normais e espaço tangente
Os vértices normais são necessários para a iluminação, e o espaço tangente é necessário para técnicas mais complicadas, como mapeamento normal.
Espaço tangente
O espaço tangente é um sistema de coordenadas em que cada vértice consiste no vetor normal, tangente e bitangente. Como esses três vetores costumam ser ortogonais uns aos outros, só precisamos armazenar dois deles e calcular o terceiro usando um produto cruzado dos outros dois no sombreador de vértice.
Esses vetores costumam ser representados usando flutuantes de 16 bits sem perda perceptível em fidelidade visual, e esse é um bom começo.
Podemos compactar ainda mais com uma técnica conhecida como QTangents (link em inglês), que armazena todo o espaço tangente em um único quatérnio. Como os quatérnios podem ser usados para representar rotações, ao pensar nos vetores do espaço tangente como vetores de coluna de uma matriz 3x3 que representa uma rotação (neste caso, do espaço do modelo para o espaço tangente), podemos fazer a conversão entre os dois. Um quatérnio pode ser tratado como dado vec4, e uma conversão de vetores de espaço tangente em um QTangent com base no artigo vinculado acima e adaptada desta implementação (link em inglês) é a seguinte:
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
O quatérnio será normalizado, e será possível compactá-lo usando SNORMs. Os SNORMs de 16 bits proporcionam uma boa precisão e economia de memória. Os SNORMs de 8 bits podem proporcionar ainda mais economia, mas podem causar artefatos em materiais altamente especulares. Faça o teste e veja o que funciona melhor para seus recursos. A codificação do quatérnio fica assim:
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
Para decodificar o quatérnio no sombreador de vértice, adaptado daqui(link em inglês):
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| Formato | Tamanho | |
|---|---|---|
| Antes | vec3<float32> + vec3<float32> + vec3<float32> |
36 bytes |
| Depois | vec4<SNORM16> |
8 bytes |
Somente normais
Se você só precisa armazenar vetores normais, há uma abordagem diferente que pode gerar mais economia: usar o mapeamento octaédrico de vetores unitários, em vez de coordenadas cartesianas para compactar o vetor normal. O mapeamento octaédrico funciona projetando uma esfera unitária em um octaedro e, em seguida, projetando o octaedro em um plano 2D. O resultado é que você pode representar qualquer vetor normal usando apenas dois números. Esses dois números podem ser considerados coordenadas de textura que usamos para "testar" o plano 2D em que a esfera foi projetada, o que nos permite recuperar o vetor original. Esses dois números podem então ser armazenados em um SNORM8.

Figura 2: mapeamento octaédrico visualizado (fonte)
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
A descompactação no sombreador de vértice (para converter de volta para coordenadas cartesianas) é barata. Na maioria dos dispositivos móveis modernos, não observamos nenhuma grande degradação no desempenho ao implementar essa técnica. A descompactação no sombreador de vértice:
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
Essa abordagem também pode ser usada para armazenar todo o espaço tangente, usando essa técnica para armazenar o vetor normal e tangente usando vec2<SNORM8>, mas será preciso encontrar uma maneira de armazenar a direção da bitangente (necessária para o cenário comum em que há coordenadas UV espelhadas em um modelo). Uma forma de implementar isso é mapear um componente da codificação vetorial tangente para ser sempre positivo e, em seguida, inverter o sinal, se você precisar virar a direção da bitangente e verificar isso no sombreador de vértice:
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| Formato | Tamanho | |
|---|---|---|
| Antes | vec3<float32> |
12 bytes |
| Depois | vec2<SNORM8> |
2 bytes |
Coordenadas UV do vértice
As coordenadas UV, usadas para mapeamento de textura (entre outras coisas), normalmente são armazenadas usando flutuantes de 32 bits. Compactá-las com pontos flutuantes de 16 bits gera problemas de precisão para texturas maiores que 1.024 x 1.024. A precisão de ponto flutuante entre [0,5, 1,0] significa que os valores serão incrementados em mais de 1 pixel.
A melhor abordagem é usar números inteiros normalizados não assinados (UNORM, na sigla em inglês), especificamente UNORM16. Isso fornece distribuição uniforme em todo o intervalo de coordenadas da textura, sendo compatível com texturas de até 65.536 x 65.536. Isso pressupõe que as coordenadas de textura estão dentro do intervalo [0,0, 1,0] por elemento, o que pode não ser o caso, dependendo da malha. Por exemplo, as paredes podem usar coordenadas de textura que vão além de 1,0, portanto, tenha isso em mente ao analisar essa técnica. A função de conversão seria esta:
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| Formato | Tamanho | |
|---|---|---|
| Antes | vec2<float32> |
8 bytes |
| Depois | vec2<UNORM16> |
4 bytes |
Resultados da compactação de vértices
Essas técnicas de compactação de vértices reduziram em 66% o armazenamento de memória, passando de 48 para 16 bytes. Isso se manifestou como:
- Largura de banda de leitura da memória do vértice:
- Agrupamento por classes: de 27 GB/s para 9 GB/s
- Renderização: de 4,5 B/s para 1,5 GB/s
- Paradas de busca de vértices:
- Agrupamento por classes: de 50% para 0%
- Renderização: de 90% para 90%
- Média de bytes/vértices:
- Agrupamento por classes: de 48 B para 16 B
- Renderização: de 52 B para 18 B
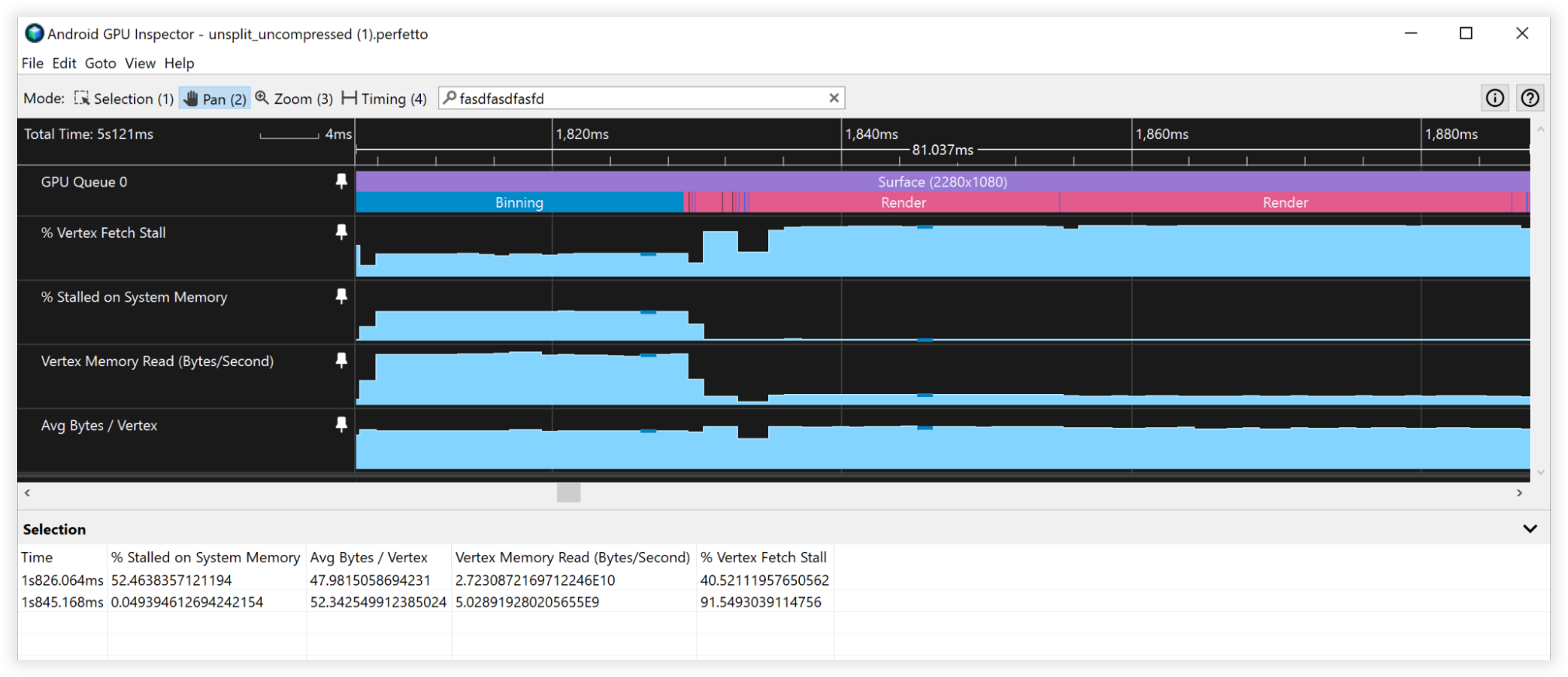
Figura 3: visualização do Android GPU Inspector de vértices não compactados
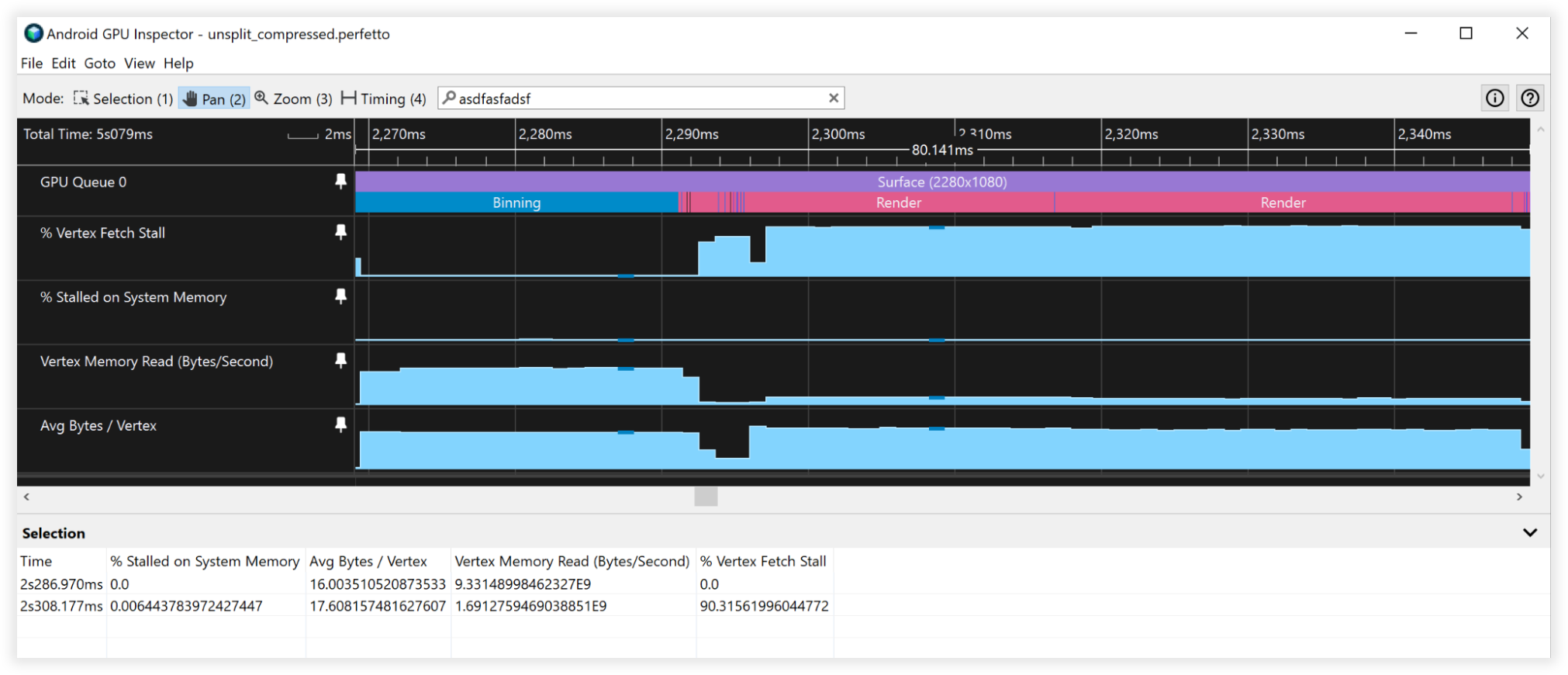
Figura 4: visualização do Android GPU Inspector de vértices compactados
Divisão de fluxo de vértices
A divisão de fluxo otimiza a organização dos dados no buffer do vértice. Essa é uma otimização de desempenho de cache que faz uma diferença nas GPUs baseadas em blocos normalmente encontradas em dispositivos Android, principalmente durante a etapa de vinculação do processo de renderização.
As GPUs baseadas em blocos criam um sombreador que calcula as coordenadas do dispositivo normalizado com base no sombreador de vértice fornecido para fazer o agrupamento. Ele é executado primeiro em todos os vértices do cenário, visíveis ou não. Portanto, manter os dados de posição do vértice contíguos na memória é uma grande vantagem. Em outros lugares, esse layout de fluxo de vértices pode ser benéfico para passagens de sombra, já que, normalmente, você só precisa de dados de posição para cálculos de sombra, bem como para pré-passagens de profundidade, que é uma técnica usada normalmente para renderização em console/computador. Esse layout de fluxo de vértices pode ser uma vitória para várias classes do mecanismo de renderização.
A divisão de fluxo envolve a configuração do buffer de vértice com uma seção contígua de dados de posição de vértice e outra seção contendo atributos de vértice intercalado. A maioria dos aplicativos geralmente configura seus buffers intercalando totalmente todos os atributos. Este recurso visual explica a diferença:
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
A análise de como a GPU busca dados de vértices nos ajuda a entender os benefícios da divisão de fluxo. Pressupondo o seguinte, apenas para fins de argumentação:
- Linhas de cache de 32 bytes (tamanho muito comum)
- Formato de vértice que consiste em:
- Posição, vec3<float32> = 12 bytes
- Normal vec3<float32> = 12 bytes
- Coordenadas UV vec2<float32> = 8 bytes
- Tamanho total = 32 bytes
Quando a GPU busca dados da memória para agrupamento por classes, ela extrai uma linha de cache de 32 bytes na qual operar. Sem a divisão do fluxo de vértices, ela utilizará somente os primeiros 12 bytes dessa linha de cache para agrupamento por classes e descartará os outros 20 bytes ao buscar o próximo vértice. Com a divisão de fluxo de vértice, as posições do vértice serão contíguas na memória, portanto, quando essa parte de 32 bytes for colocada no cache, ela conterá duas posições inteiras do vértice para operar antes de voltar à memória principal para buscar mais. Isso significa que será duas vezes melhor.
Agora, se combinarmos a divisão do fluxo de vértice com a compactação de vértice, reduziremos o tamanho de uma única posição de vértice para 6 bytes, de modo que uma única linha de cache de 32 bytes extraída da memória do sistema terá 5 posições de vértice inteiras para operar. Uma melhoria de cinco vezes.
Resultados da divisão de fluxo de vértices
- Largura de banda de leitura da memória do vértice:
- Agrupamento por classes: de 27 GB/s para 6,5 GB/s
- Renderização: de 4,5 GB/s para 4,5 GB/s
- Paradas de busca de vértices:
- Agrupamento por classes: de 40% para 0%
- Renderização: de 90% para 90%
- Média de bytes/vértices:
- Agrupamento por classes: de 48 B para 12 B
- Renderização: de 52 B para 52 B

Figura 5: visualização do Android GPU Inspector de fluxos de vértices não divididos
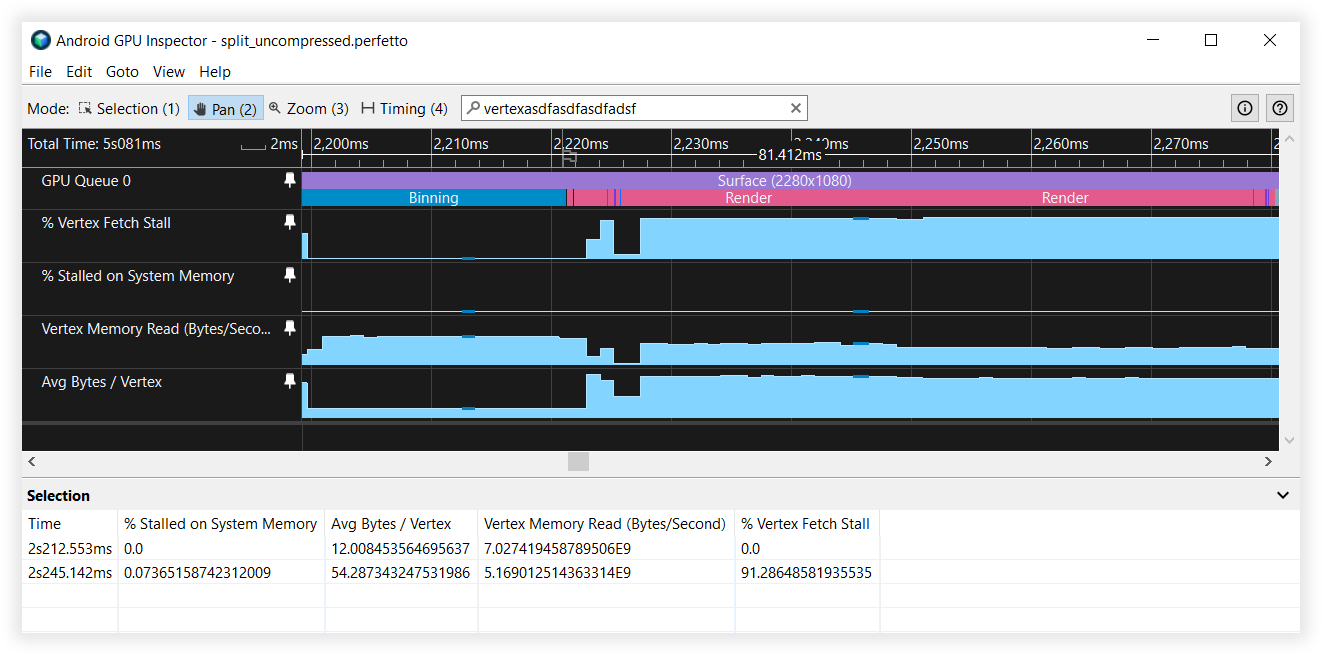
Figura 6: visualização do Android GPU Inspector de fluxos de vértices divididos
Resultados compostos
- Largura de banda de leitura da memória do vértice:
- Agrupamento por classes: de 25 GB/s para 4,5 GB/s
- Renderização: de 4,5 GB/s para 1,7 GB/s
- Paradas de busca de vértices:
- Agrupamento por classes: de 41% para 0%
- Renderização: de 90% para 90%
- Média de bytes/vértices:
- Agrupamento por classes: de 48 B para 8 B
- Renderização: de 52 B para 19 B

Figura 7: visualização do Android GPU Inspector de fluxos de vértices não divididos e não compactados
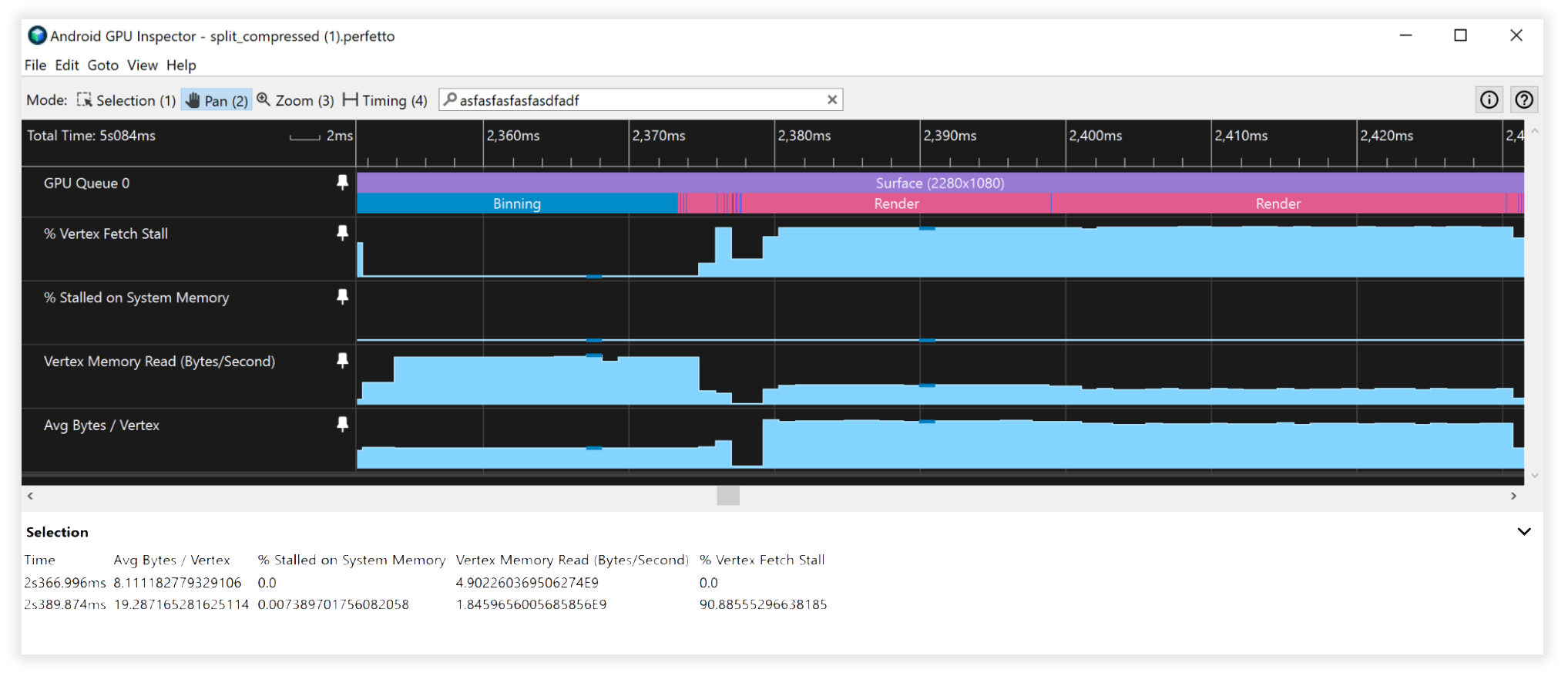
Figura 8: visualização do Android GPU Inspector de fluxos de vértices divididos e compactados
Outras considerações
Dados de buffer do índice de 16 x 32 bits
- Sempre divida/separe malhas para que se encaixem em um buffer de índice de 16 bits (máximo de 65.536 vértices únicos). Isso ajudará na renderização indexada em dispositivos móveis, já que é mais barato buscar dados de vértices, além de consumir menos energia.
Formatos incompatíveis de atributos do buffer de vértices
- Os formatos de vértice SSCALED não são amplamente compatíveis com dispositivos móveis. Quando usados, podem trazer um custo elevado ao desempenho em drivers que tentam emular esses dispositivos, se não forem compatíveis com o hardware. Prefira sempre o SNORM e pague o custo insignificante do ALU para descompactar.
