앱이 2D 사용자 인터페이스로 구성되는지 아니면 대형 3D 오픈 월드 게임인지 여부와 무관하게 모든 그래픽 애플리케이션의 성능에서 양호한 버텍스 데이터 레이아웃과 압축은 필수입니다. 수십 개의 인기 Android 게임에 관해 Android GPU 검사기의 프레임 프로파일러를 사용한 내부 테스트를 통해 버텍스 데이터 관리를 개선할 수 있는 작업이 많다는 것을 확인할 수 있습니다. 버텍스 데이터가 모든 버텍스 속성에 대해 전체 정밀도 32비트 부동 소수점 수 값을 사용하고, 전체 인터리브 속성으로 형식이 지정된 구조 배열을 사용하는 버텍스 버퍼 레이아웃을 사용하는 것이 일반적입니다.
이 문서에서는 다음 기법을 사용하여 Android 애플리케이션의 그래픽 성능을 최적화하는 방법을 설명합니다.
- 버텍스 압축
- 버텍스 스트림 분할
이러한 기법을 구현하면 버텍스 메모리 대역폭 사용량을 최대 50% 개선하고, CPU와의 메모리 버스 경합과 시스템 메모리의 중단을 줄이고, 배터리 수명을 개선할 수 있습니다. 그리고 이 모든 것은 개발자와 최종 사용자 모두에게 유익합니다.
제공된 모든 데이터는 Pixel 4에서 실행되는 최대 19,000,000개의 버텍스가 포함된 정적 장면 예시에서 제공됩니다.

그림 1: 6개의 링과 1,900만 개의 꼭짓점이 있는 샘플 장면
버텍스 압축
버텍스 압축은 런타임 도중 및 저장 시 모두에서 버텍스 데이터의 크기를 줄이기 위해 효율적인 패키징을 사용하는 손실 압축 기법의 포괄적인 용어입니다. 버텍스의 크기를 줄이면 (대역폭 컴퓨팅을 통해) GPU의 메모리 대역폭을 줄이고, 캐시 사용률을 높이고, 레지스터 제거 위험을 줄일 수 있는 등 여러 가지 이점이 있습니다.
버텍스 압축의 일반적인 접근법은 다음과 같습니다.
- 버텍스 데이터 속성의 숫자 정밀도 감소(예: 32비트 부동 소수점 수에서 16비트 부동 소수점 수)
- 다양한 형식의 속성 표현
예를 들어 버텍스가 위치(vec3), 노멀(vec3), 텍스처 좌표(vec2)에 대해 전체 32비트 부동 소수점 수를 사용하는 경우 모두 16비트 부동 소수점 수로 바꾸면 버텍스 크기가 50% 감소합니다(평균 32바이트 버텍스에서 16바이트).
버텍스 위치
버텍스 위치 데이터는 전체 정밀도 32비트 부동 소수점 값에서 대부분 메시의 절반 정밀도 16비트 부동 소수점 값으로 압축할 수 있으며, 거의 모든 휴대기기의 하드웨어에서 절반 부동 소수점 수가 지원됩니다. float32에서 float16으로의 변환 함수는 다음과 같습니다(이 가이드에서 조정).
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
이 방식에는 버텍스가 원점에서 멀어질수록 정밀도가 떨어진다는 제한이 있습니다. 따라서 공간적으로 매우 큰 메시(요소가 1,024개를 초과하는 버텍스)에는 적합하지 않습니다. 메시를 더 작은 청크로 분할하고, 모델 원점을 중심으로 각 청크를 중앙에 배치하고, 각 청크의 모든 버텍스가 부동 소수점 값의 가장 높은 정밀도를 포함하는 [-1, 1] 범위에 맞도록 조정함으로써 이 문제를 해결할 수 있습니다. 압축에 대한 의사코드는 다음과 같습니다.
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
렌더링 시 버텍스 데이터의 압축을 풀기 위해 배율 계수와 변환을 모델 매트릭스로 베이크합니다. 동일한 압축이 사용되지 않았으므로 노멀 변환에는 동일한 모델 매트릭스를 사용하지 않는 것이 좋습니다. 노멀에는 이러한 압축 해제 변환이 없는 매트릭스가 필요합니다. 또는 기본 모델 매트릭스(노멀에 대해 사용할 수 있음)를 사용한 다음 추가 압축 해제 변환을 셰이더 내의 모델 매트릭스에 적용할 수 있습니다. 예를 들면 다음과 같습니다.
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
또 다른 방법은 서명된 정규화 정수(SNORM)를 사용하는 것입니다. SNORM 데이터 유형은 부동 소수점 대신 정수를 사용하여 [-1, 1] 사이의 값을 나타냅니다. 위치에 16비트 SNORM을 사용하면 균일하지 않은 분포라는 단점 없이 float16과 동일한 메모리 절감 효과를 얻을 수 있습니다. SNORM 사용에 권장되는 구현은 다음과 같습니다.
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| 형식 | 크기 | |
|---|---|---|
| 전 | vec4<float32> |
16바이트 |
| 후 | vec3<float16/SNORM16> |
6바이트 |
버텍스 노멀과 탄젠트 공간
조명에는 버텍스 노멀이 필요하고, 노멀 매핑과 같이 더 복잡한 기법에는 탄젠트 공간이 필요합니다.
탄젠트 공간
탄젠트 공간은 모든 버텍스가 노멀, 탄젠트, 바이탄젠트 벡터로 구성된 좌표 체계입니다. 이 세 가지 벡터는 일반적으로 서로 연결되므로 두 개의 벡터만 저장하고 버텍스 셰이더에서 다른 둘의 교차 곱을 취하여 세 번째 벡터를 계산할 수 있습니다.
이러한 벡터는 일반적으로 시각적 충실도에 눈에 띄는 손실 없이 16비트 부동 소수점을 사용하여 표현될 수 있으므로, 좋은 시작점이 될 것입니다!
전체 탄젠트 공간을 단일 사원수에 저장하는 QTangents라는 기법을 사용하여 추가 압축이 가능합니다. 사원수는 회전을 나타내는 데 사용될 수 있으므로 탄젠트 공간 벡터를 회전(이 경우 모델 공간에서 탄젠트 공간으로 변환)을 나타내는 3x3 매트릭스의 열 벡터로 간주하여 이 둘 사이에서 변환할 수 있습니다. 사원수는 데이터 측면에서 vec4로 취급할 수 있으며, 위의 링크 및 여기에서 구현 내용에 맞게 조정된 문서에 따라 탄젠트 공간 벡터에서 QTangent로 변환하는 방법은 다음과 같습니다.
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
사원수는 정규화되며 SNORM을 사용하여 압축할 수 있습니다. 16비트 SNORM은 뛰어난 정밀도와 메모리 절감 효과를 제공합니다. 8비트 SNORM을 사용하면 더 많은 비용 절감 효과를 얻을 수 있지만 높은 반사율로 인한 아티팩트가 발생할 수 있습니다. 두 가지를 모두 사용해 보고 어느 것이 애셋에 가장 적합한지 살펴볼 수 있습니다. 사원수 인코딩은 다음과 같습니다.
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
버텍스 셰이더의 사원수를 디코딩하는 방법은 다음과 같습니다(여기에서 조정).
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| 형식 | 크기 | |
|---|---|---|
| 전 | vec3<float32> + vec3<float32> + vec3<float32> |
36바이트 |
| 후 | vec4<SNORM16> |
8바이트 |
노멀 전용
노멀 벡터만 저장해야 하는 경우 더 많은 비용을 절감할 수 있는 다른 방법이 있습니다. 노멀 벡터를 압축하는 데 데카르트식 좌표가 아닌 단위 벡터의 8면체 매핑을 사용하면 됩니다. 8면체 매핑은 단위 구체를 8면체에 투영하고 8면체를 2D 평면으로 투영하는 방식으로 작동합니다. 따라서 숫자 두 개만 사용하여 노멀 벡터를 나타낼 수 있습니다. 이 두 숫자는 구체를 투영한 2D 평면을 '샘플링'하여 원래 벡터를 복구할 수 있는 텍스처 좌표로 생각할 수 있습니다. 그러면 이 두 숫자는 SNORM8에 저장될 수 있습니다.

그림 2: 8면체 매핑 시각화 (출처)
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
버텍스 셰이더의 압축 해제(데카르트식 좌표로 다시 변환)는 비용이 저렴합니다. 대부분의 최신 모바일 기기에서 이 기법을 구현할 때 중대한 성능 저하가 발견되지 않았습니다. 버텍스 셰이더의 압축 해제는 다음과 같습니다.
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
이 접근 방식을 사용하면 vec2<SNORM8>을 사용하여 노멀 및 탄젠트 벡터를 저장하는 데 사용하는 전체 탄젠트 공간을 저장할 수 있지만 비트탄젠트(모델에 UV 좌표를 미러링한 일반적인 시나리오에서 필요)의 방향을 저장할 방법을 찾아야 합니다. 이를 구현하는 한 가지 방법은 탄젠트 벡터 인코딩의 구성요소를 항상 양수로 매핑한 다음, 비트탄젠트 방향을 뒤집고 버텍스 셰이더에서 확인해야 하는 경우 부호를 뒤집는 것입니다.
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| 형식 | 크기 | |
|---|---|---|
| 전 | vec3<float32> |
12바이트 |
| 후 | vec2<SNORM8> |
2바이트 |
버텍스 UV 좌표
텍스처 매핑에 사용되는 UV 좌표는 일반적으로 32비트 부동 소수점 수를 사용하여 저장됩니다. 16비트 부동 소수점 수로 압축하면 1024x1024보다 큰 텍스처에 정밀도 문제가 발생합니다. [0.5, 1.0] 사이의 부동 소수점 정밀도는 값이 1픽셀 이상 증가한다는 것을 의미합니다.
더 나은 방법은 부호가 없는 정규화 정수(UNORM), 특히 UNORM16을 사용하는 것입니다. 이 기능은 전체 텍스처 좌표 범위에 걸쳐 균일한 분포를 제공하여 최대 65536x65536까지 텍스처를 지원합니다. 이는 텍스처 좌표가 요소당 [0.0, 1.0] 범위 내에 있다고 가정합니다. 따라서 메시에 따라 다를 수 있습니다(예: 벽은 1.0을 벗어난 래핑 텍스처 좌표를 사용할 수 있음). 이 기법을 검토할 때는 이 점을 주의하세요. 변환 함수는 다음과 같습니다.
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| 형식 | 크기 | |
|---|---|---|
| 전 | vec2<float32> |
8바이트 |
| 후 | vec2<UNORM16> |
4바이트 |
버텍스 압축 결과
이러한 버텍스 압축 기법을 통해 버텍스 메모리 스토리지가 66% 감소하여 48바이트에서 16바이트로 감소했습니다. 결과는 다음과 같습니다.
- 버텍스 메모리 읽기 대역폭:
- 비닝: 27GB/s~9GB/s
- 렌더링: 4.5B/s~1.5GB/s
- 버텍스 가져오기 중단:
- 비닝: 50%~0%
- 렌더링: 90%~90%
- 평균 바이트/버텍스:
- 비닝: 48B~16B
- 렌더링: 52B~18B
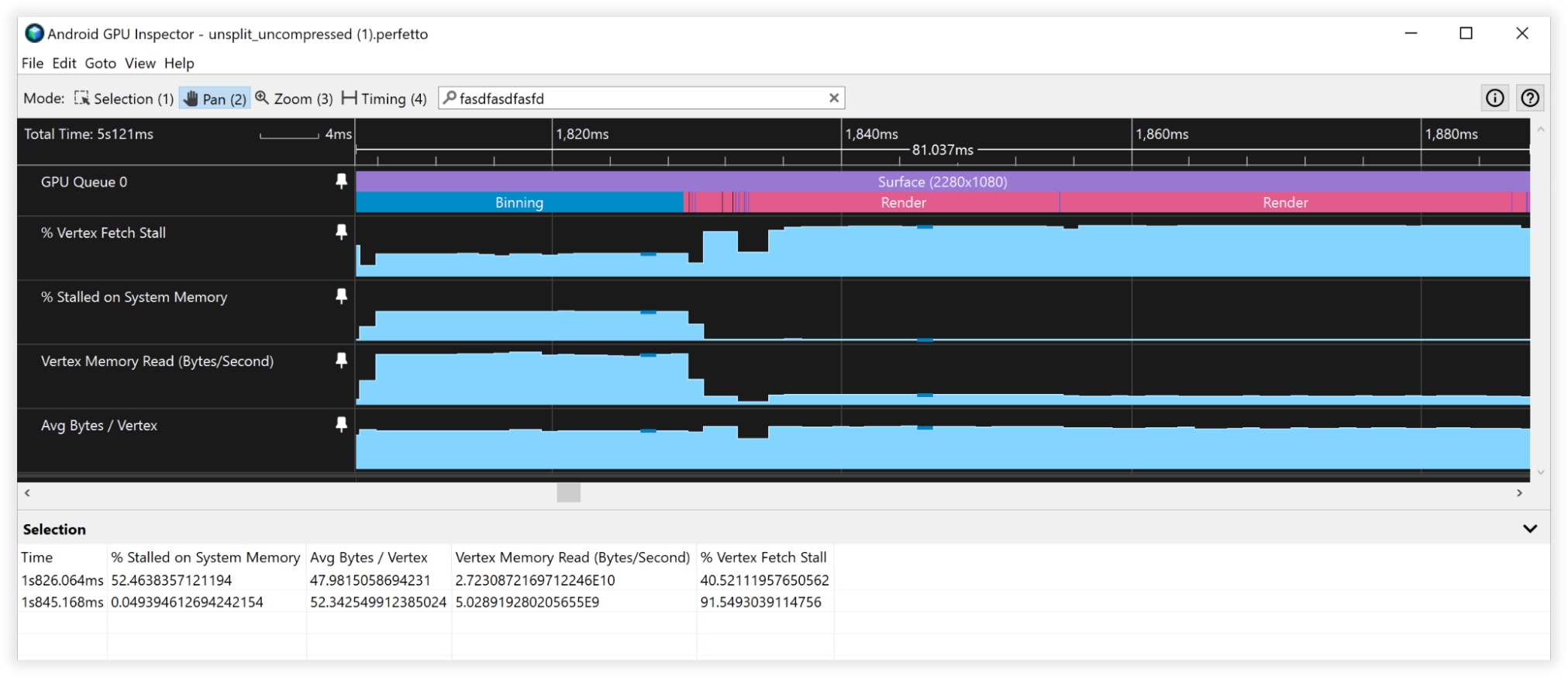
그림 3: 압축되지 않은 꼭짓점의 Android GPU 검사기 뷰
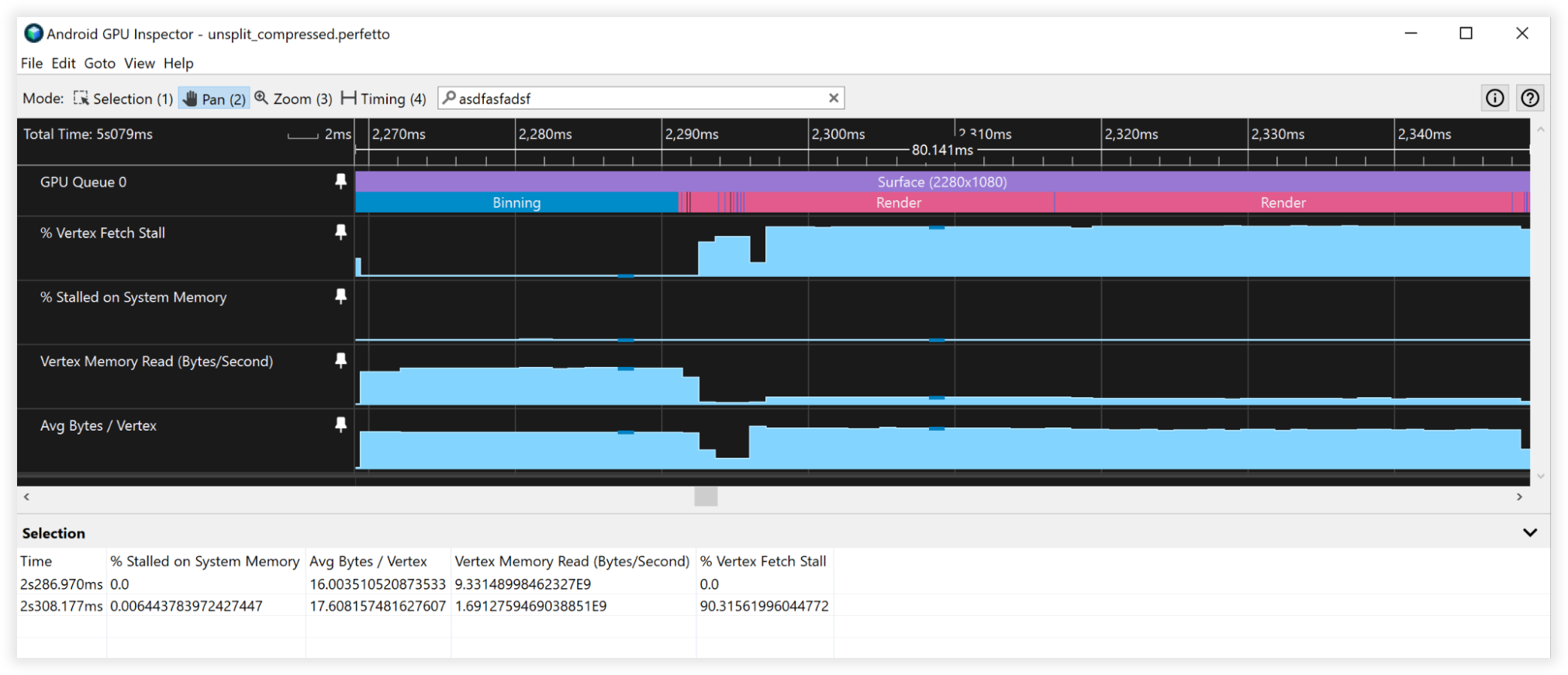
그림 4: 압축된 버텍스의 Android GPU 검사기 뷰
버텍스 스트림 분할
버텍스 스트림 분할은 버텍스 버퍼의 데이터 구성을 최적화합니다. 이는 Android 기기에서 흔히 볼 수 있는 타일 기반 GPU, 특히 렌더링 프로세스의 비닝 단계 도중 차이를 만드는 캐시 성능 최적화입니다.
타일 기반 GPU는 제공된 버텍스 셰이더를 기반으로 하는 정규화된 기기 좌표를 계산하여 비닝을 수행하는 셰이더를 만듭니다. 이 설정은 표시 여부와 무관하게 장면의 모든 버텍스에서 먼저 실행됩니다. 따라서 버텍스 위치 데이터를 메모리 근처에 유지하는 것은 큰 이점입니다. 이 버텍스 스트림 레이아웃이 유용할 수 있는 다른 위치는 섀도우 패스입니다. 일반적으로 콘솔/데스크톱 렌더링에 사용되는 기법인 심도 프리패스는 물론 섀도우 계산에 위치 데이터가 필요하기 때문이며, 이 버텍스 스트림 레이아웃은 렌더링 엔진의 여러 클래스에서 유용할 수 있습니다.
스트림 분할은 버텍스 위치 데이터의 인접한 섹션과 인터리브 버텍스 속성이 포함된 다른 섹션으로 버텍스 버퍼를 설정하는 작업이 포함됩니다. 대부분의 애플리케이션은 일반적으로 버퍼를 모든 속성의 전체 인터리빙으로 설정합니다. 시각적 차이를 이렇게 설명할 수 있습니다.
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
GPU가 버텍스 데이터를 가져오는 방법을 살펴보면 스트림 분할의 이점을 이해할 수 있습니다. 인수를 고려하는 경우는 다음과 같습니다.
- 32바이트 캐시 라인(상당한 공통 크기)
- 다음으로 구성된 버텍스 형식:
- 위치, vec3<float32> = 12바이트
- 노멀 vec3<float32> = 12바이트
- UV 좌표 vec2<float32> = 8바이트
- 총 크기 = 32바이트
GPU는 비닝을 위해 메모리에서 데이터를 가져올 때 연산할 32바이트 캐시 라인을 가져옵니다. 버텍스 스트림 분할을 사용하지 않으면 실제로 비닝에 이 캐시 라인의 처음 12바이트만 사용하고 나머지 20바이트는 다음 버텍스를 가져올 때 삭제합니다. 버텍스 스트림 분할을 사용하면 버텍스 위치가 메모리에 인접하고 따라서 32바이트 청크를 캐시로 가져올 때, 기본 메모리로 돌아가게 되기 전에 연산하는 두 개의 버텍스 위치가 포함되므로 2배 향상됩니다.
이제 버텍스 스트림 분할을 버텍스 압축과 결합하면 단일 버텍스 위치의 크기를 6바이트로 줄입니다. 따라서 시스템 메모리에서 가져온 단일 32바이트 캐시 라인에는 연산할 버텍스 5개가 있으므로 5배 향상됩니다.
버텍스 스트림 분할 결과
- 버텍스 메모리 읽기 대역폭:
- 비닝: 27GB/s~6.5GB/s
- 렌더링: 4.5GB/s~4.5GB/s
- 버텍스 가져오기 중단:
- 비닝: 40%~0%
- 렌더링: 90%~90%
- 평균 바이트/버텍스:
- 비닝: 48B~12B
- 렌더링: 52B~52B

그림 5: 분할되지 않은 버텍스 스트림의 Android GPU 검사기 뷰
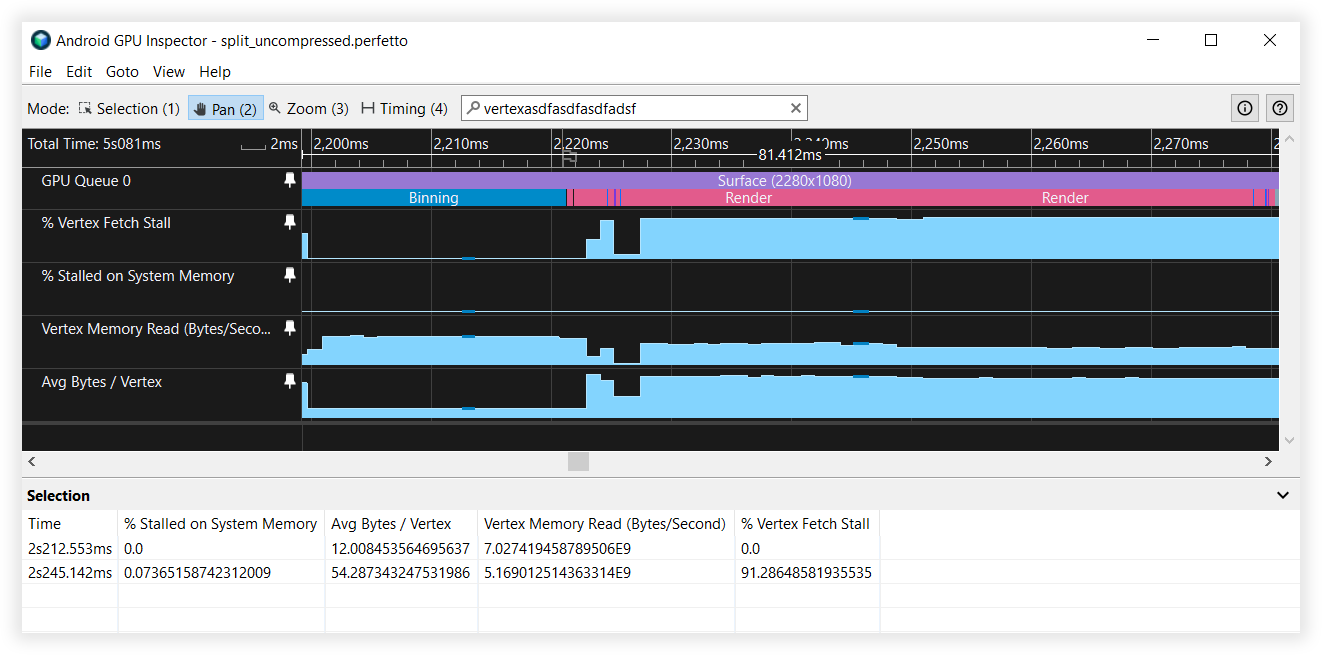
그림 6: 분할된 버텍스 스트림의 Android GPU 검사기 뷰
복합 결과
- 버텍스 메모리 읽기 대역폭:
- 비닝: 25GB/s~4.5GB/s
- 렌더링: 4.5GB/s~1.7GB/s
- 버텍스 가져오기 중단:
- 비닝: 41%~0%
- 렌더링: 90%~90%
- 평균 바이트/버텍스:
- 비닝: 48B~8B
- 렌더링: 52B~19B

그림 7: 분할되지 않은 비압축 버텍스 스트림의 Android GPU 검사기 뷰
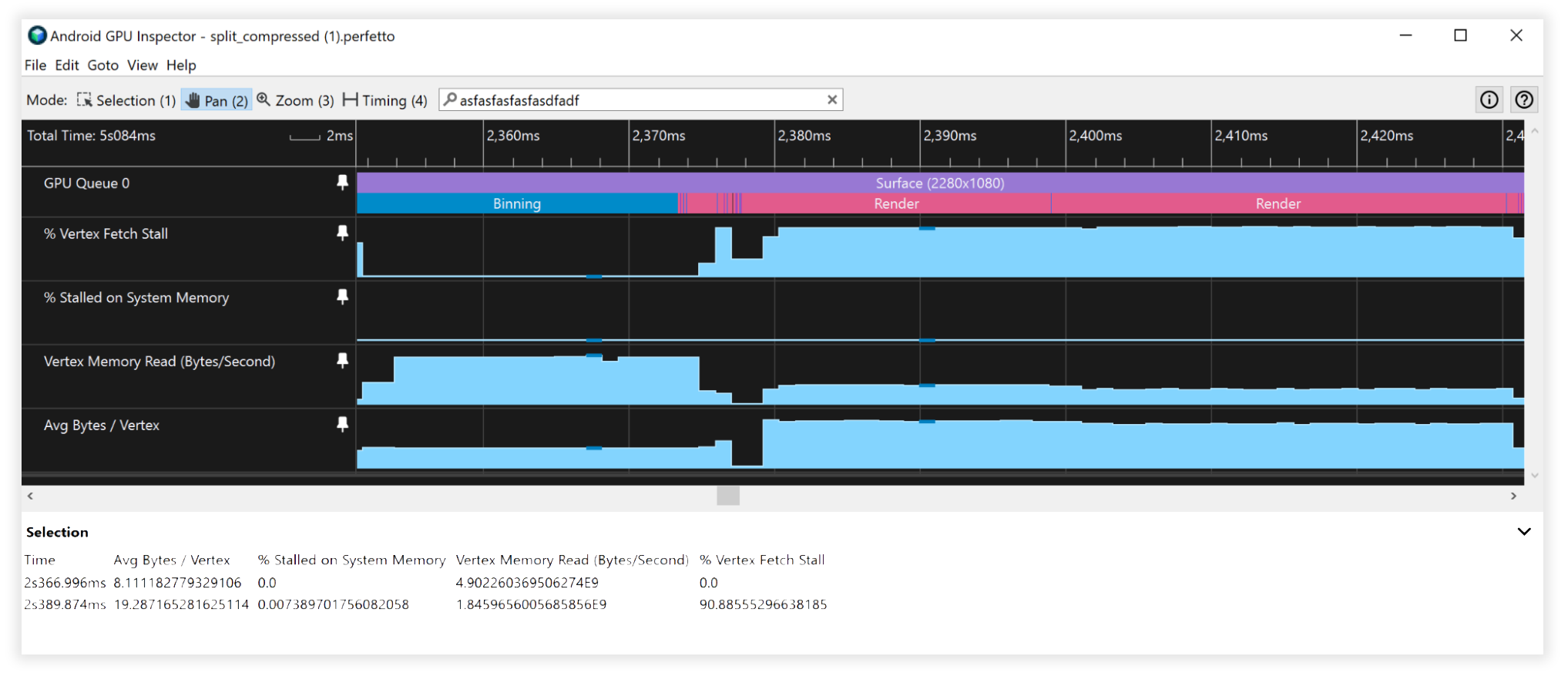
그림 8: 분할된 압축된 버텍스 스트림의 Android GPU 검사기 뷰
추가 고려사항
16비트 vs. 32비트 색인 버퍼 데이터
- 항상 16비트 색인 버퍼에 맞도록 메시를 항상 분할/청크합니다(최대 고유 버텍스 65,536개). 이렇게 하면 모바일에서 색인이 생성되는 렌더링에 도움이 됩니다. 더 저렴하게 버텍스 데이터를 가져오고 전력 소모도 적습니다.
지원되지 않는 버텍스 버퍼 속성 형식
- SSCALED 버텍스 형식은 모바일에서 널리 지원되지 않으며, 이 경우 하드웨어 지원이 없으면 이를 에뮬레이션하는 드라이버에서 성능 저하가 발생할 수 있습니다. 항상 SNORM으로 변환하고 미미한 ALU 비용을 지불하여 압축을 해제하세요.
