چیدمان و فشردهسازی دادههای راس خوب برای عملکرد هر برنامه گرافیکی ضروری است، چه برنامهای از رابطهای کاربری دوبعدی تشکیل شده باشد یا یک بازی بزرگ جهان باز سه بعدی باشد. آزمایش داخلی با نمایه قاب Android GPU Inspector در ده ها بازی برتر اندروید نشان می دهد که می توان کارهای زیادی برای بهبود مدیریت داده های راس انجام داد. مشاهده کردهایم که معمولاً برای دادههای راس استفاده از دقت کامل، مقادیر شناور 32 بیتی برای همه ویژگیهای راس، و طرحبندی بافر رأس که از آرایهای از ساختارهای قالببندیشده با ویژگیهای کاملاً درونلایهشده استفاده میکند، رایج است.
این مقاله نحوه بهینه سازی عملکرد گرافیکی برنامه اندروید خود را با استفاده از تکنیک های زیر مورد بحث قرار می دهد:
- فشرده سازی راس
- تقسیم جریان راس
اجرای این تکنیک ها می تواند استفاده از پهنای باند حافظه را تا 50% بهبود بخشد، اختلاف گذرگاه حافظه با CPU را کاهش دهد، حافظه سیستم را کاهش دهد و عمر باتری را بهبود بخشد. همه آنها هم برای توسعه دهندگان و هم برای کاربران نهایی برنده هستند!
تمام دادههای ارائهشده از یک صحنه ثابت مثالی حاوی 19,000,000 رأس در حال اجرا بر روی Pixel 4 میآیند:

شکل 1: نمونه صحنه با 6 حلقه و راس 19 متر
فشرده سازی راس
فشردهسازی راس یک اصطلاح کلی برای تکنیکهای فشردهسازی با تلفات است که از بستهبندی کارآمد برای کاهش اندازه دادههای راس هم در زمان اجرا و هم در ذخیرهسازی استفاده میکند. کاهش اندازه رئوس چندین مزیت دارد، از جمله کاهش پهنای باند حافظه در GPU (با مبادله محاسبات با پهنای باند)، بهبود استفاده از حافظه پنهان، و به طور بالقوه کاهش خطر ریختن رجیسترها.
رویکردهای رایج برای فشرده سازی ورتکس عبارتند از:
- کاهش دقت عددی ویژگیهای دادههای راس (مثلاً شناور ۳۲ بیتی به شناور ۱۶ بیتی)
- نمایش ویژگی ها در قالب های مختلف
به عنوان مثال، اگر یک راس از شناورهای کامل 32 بیتی برای موقعیت (vec3)، معمولی (vec3) و مختصات بافت (vec2) استفاده کند، جایگزینی همه اینها با شناورهای 16 بیتی، اندازه راس را تا 50٪ کاهش می دهد (16 بایت در روز). راس متوسط 32 بایت).
موقعیت های راس
داده های موقعیت راس را می توان از مقادیر ممیز شناور 32 بیتی با دقت کامل تا مقادیر نقطه شناور نیمه دقیق 16 بیتی در اکثریت قریب به اتفاق مش ها فشرده کرد، و نیم شناورها در سخت افزار تقریباً در همه دستگاه های تلفن همراه پشتیبانی می شوند. یک تابع تبدیل که از float32 به float16 میرود به این شکل است ( برگرفته از این راهنما ):
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
محدودیتی برای این رویکرد وجود دارد. با دورتر شدن راس از مبدأ، دقت کاهش مییابد و آن را برای مشهایی که از نظر فضایی بسیار بزرگ هستند (رئوسهایی که دارای عناصری فراتر از 1024 هستند) مناسب نیست. می توانید با تقسیم یک مش به تکه های کوچکتر، وسط هر تکه حول مبدا مدل، و مقیاس بندی به گونه ای که تمام رئوس هر تکه در محدوده [-1، 1] قرار گیرند، که دارای بالاترین دقت برای نقطه شناور است، این مشکل را برطرف کنید. ارزش ها شبه کد فشرده سازی به صورت زیر است:
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
شما ضریب مقیاس و ترجمه را در ماتریس مدل میسازید تا دادههای راس را هنگام رندر از حالت فشرده خارج کنید. به خاطر داشته باشید که نمی خواهید از همین ماتریس مدل برای تبدیل نرمال ها استفاده کنید، زیرا فشرده سازی یکسانی اعمال نمی شود. شما به یک ماتریس بدون این تبدیلهای رفع فشار برای نرمالها نیاز دارید، یا میتوانید از ماتریس مدل پایه (که میتوانید برای نرمالها استفاده کنید) استفاده کنید و سپس تبدیلهای رفع فشار اضافی را به ماتریس مدل در سایهزن اعمال کنید. یک مثال:
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
رویکرد دیگر شامل استفاده از اعداد صحیح عادی شده امضا شده (SNORM) است. انواع داده SNORM از اعداد صحیح به جای ممیز شناور برای نمایش مقادیر بین [-1، 1] استفاده می کنند. استفاده از یک SNORM 16 بیتی برای موقعیت ها به شما همان ذخیره حافظه float16 را بدون اشکالات توزیع های غیر یکنواخت می دهد. پیاده سازی که ما برای استفاده از SNORM توصیه می کنیم به صورت زیر است:
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| قالب | اندازه | |
|---|---|---|
| قبل از | vec4< float32 > | 16 بایت |
| بعد از | vec3< float16/SNORM16 > | 6 بایت |
نرمال های راس و فضای مماس
Vertex Normals برای نورپردازی مورد نیاز است و فضای مماس برای تکنیکهای پیچیدهتر مانند نقشهبرداری معمولی مورد نیاز است.
فضای مماس
فضای مماس یک سیستم مختصاتی است که در آن هر رأس از بردار عادی، مماس و دو مماس تشکیل شده است. از آنجایی که این سه بردار معمولاً متعامد با یکدیگر هستند، ما فقط باید دو تا از آنها را ذخیره کنیم و میتوانیم سومی را با گرفتن ضرب ضربدری از دو بردار دیگر در سایهزن راس محاسبه کنیم.
این بردارها معمولاً می توانند با استفاده از شناورهای 16 بیتی بدون هیچ گونه افت ادراکی در وفاداری بصری نمایش داده شوند، بنابراین مکان خوبی برای شروع است!
ما میتوانیم با تکنیکی به نام QTangents که کل فضای مماس را در یک کواترنیون ذخیره میکند، بیشتر فشردهسازی کنیم. از آنجایی که از کواترنیون ها می توان برای نمایش چرخش ها استفاده کرد، با در نظر گرفتن بردارهای فضای مماس به عنوان بردارهای ستونی یک ماتریس 3x3 که نشان دهنده یک چرخش است (در این مورد از فضای مدل به فضای مماس) می توانیم بین این دو تبدیل کنیم! یک کواترنیون را می توان از نظر داده به عنوان vec4 در نظر گرفت، و تبدیل از بردارهای فضای مماس به یک QTangent بر اساس مقاله لینک شده در بالا و اقتباس از پیاده سازی در اینجا به شرح زیر است:
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
کواترنیون نرمال می شود و شما می توانید آن را با استفاده از SNORM فشرده کنید. SNORM های 16 بیتی دقت و حافظه خوبی را ذخیره می کنند. SNORM های 8 بیتی می توانند حتی بیشتر صرفه جویی کنند، اما ممکن است باعث ایجاد مصنوعات در مواد بسیار خاص شوند. میتوانید هر دو را امتحان کنید و ببینید چه چیزی برای داراییهای شما بهتر است! رمزگذاری کواترنیون به صورت زیر است:
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
برای رمزگشایی کواترنیون در سایه زن راس ( از اینجا اقتباس شده است ):
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| قالب | اندازه | |
|---|---|---|
| قبل از | vec3< float32 > + vec3< float32 > + vec3< float32 > | 36 بایت |
| بعد از | vec4< SNORM16 > | 8 بایت |
فقط نرمال ها
اگر فقط نیاز به ذخیره بردارهای عادی دارید، رویکرد متفاوتی وجود دارد که می تواند منجر به صرفه جویی بیشتر شود - با استفاده از نقشه برداری هشت وجهی بردارهای واحد به جای مختصات دکارتی برای فشرده سازی بردار عادی . نقشه برداری هشت وجهی به این صورت کار می کند که یک کره واحد را به یک هشت ضلعی نشان می دهد و سپس هشت وجهی را به یک صفحه دو بعدی نشان می دهد. نتیجه این است که شما می توانید هر بردار معمولی را تنها با استفاده از دو عدد نشان دهید. این دو عدد را میتوان بهعنوان مختصات بافتی در نظر گرفت که ما برای «نمونهبرداری» از صفحه دوبعدی که کره را روی آن نمایش دادهایم، استفاده میکنیم و به ما امکان میدهد بردار اصلی را بازیابی کنیم. سپس این دو عدد را می توان در SNORM8 ذخیره کرد.
شکل 2: نقشه برداری هشت وجهی بصری شده ( منبع )
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
رفع فشار در سایه زن راس (برای تبدیل مجدد به مختصات دکارتی) ارزان است. با اکثر دستگاه های تلفن همراه مدرن، ما در هنگام اجرای این تکنیک شاهد کاهش عملکرد عمده ای نبودیم. رفع فشار در سایه زن راس:
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
این رویکرد همچنین می تواند برای ذخیره کل فضای مماس استفاده شود، با استفاده از این تکنیک برای ذخیره بردار نرمال و مماس با استفاده از vec2< SNORM8 > اما شما باید راهی برای ذخیره جهت تانژانت پیدا کنید (برای سناریوی رایج که در آن لازم است. مختصات UV را روی یک مدل منعکس کرده اید). یکی از راههای پیادهسازی این است که یک مؤلفه از رمزگذاری بردار مماس خود را به گونهای ترسیم کنید که همیشه مثبت باشد، سپس علامت آن را برگردانید، اگر باید جهت دو تایی را برگردانید و آن را در سایهزن راس بررسی کنید:
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| قالب | اندازه | |
|---|---|---|
| قبل از | vec3< float32 > | 12 بایت |
| بعد از | vec2< SNORM8 > | 2 بایت |
مختصات UV Vertex
مختصات UV، که برای نگاشت بافت (در میان چیزهای دیگر) استفاده می شود، معمولاً با استفاده از شناورهای 32 بیتی ذخیره می شوند. فشرده سازی آنها با شناورهای 16 بیتی باعث ایجاد مشکلاتی در دقت بافت های بزرگتر از 1024x1024 می شود. دقت ممیز شناور بین [0.5، 1.0] به این معنی است که مقادیر بزرگتر از 1 پیکسل افزایش می یابد!
روش بهتر استفاده از اعداد صحیح عادی شده بدون علامت (UNORM)، به ویژه UNORM16 است. این توزیع یکنواخت را در کل محدوده مختصات بافت فراهم می کند و از بافت ها تا 65536x65536 پشتیبانی می کند! این فرض را بر این میگذارد که مختصات بافت در محدوده [0.0، 1.0] برای هر عنصر است، که ممکن است بسته به شبکه اینطور نباشد (به عنوان مثال دیوارها میتوانند از مختصات بافت بستهبندی استفاده کنند که فراتر از 1.0 است) بنابراین هنگام مشاهده این تکنیک این را در نظر داشته باشید. . تابع تبدیل به شکل زیر است:
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| قالب | اندازه | |
|---|---|---|
| قبل از | vec2< float32 > | 8 بایت |
| بعد از | vec2< UNORM16 > | 4 بایت |
نتایج فشرده سازی راس
این تکنیکهای فشردهسازی راس منجر به کاهش 66 درصدی ذخیرهسازی حافظه راس شد که از 48 بایت به 16 بایت کاهش یافت. این خود را به صورت زیر نشان داد:
- پهنای باند خواندن حافظه Vertex:
- Binning: 27GB/s تا 9GB/s
- رندر: 4.5B/s تا 1.5GB/s
- غرفه های واکشی Vertex:
- باینینگ: 50% تا 0%
- رندر: 90% تا 90%
- میانگین بایت/راس:
- Binning: 48B تا 16B
- رندر: 52 تا 18 بایت
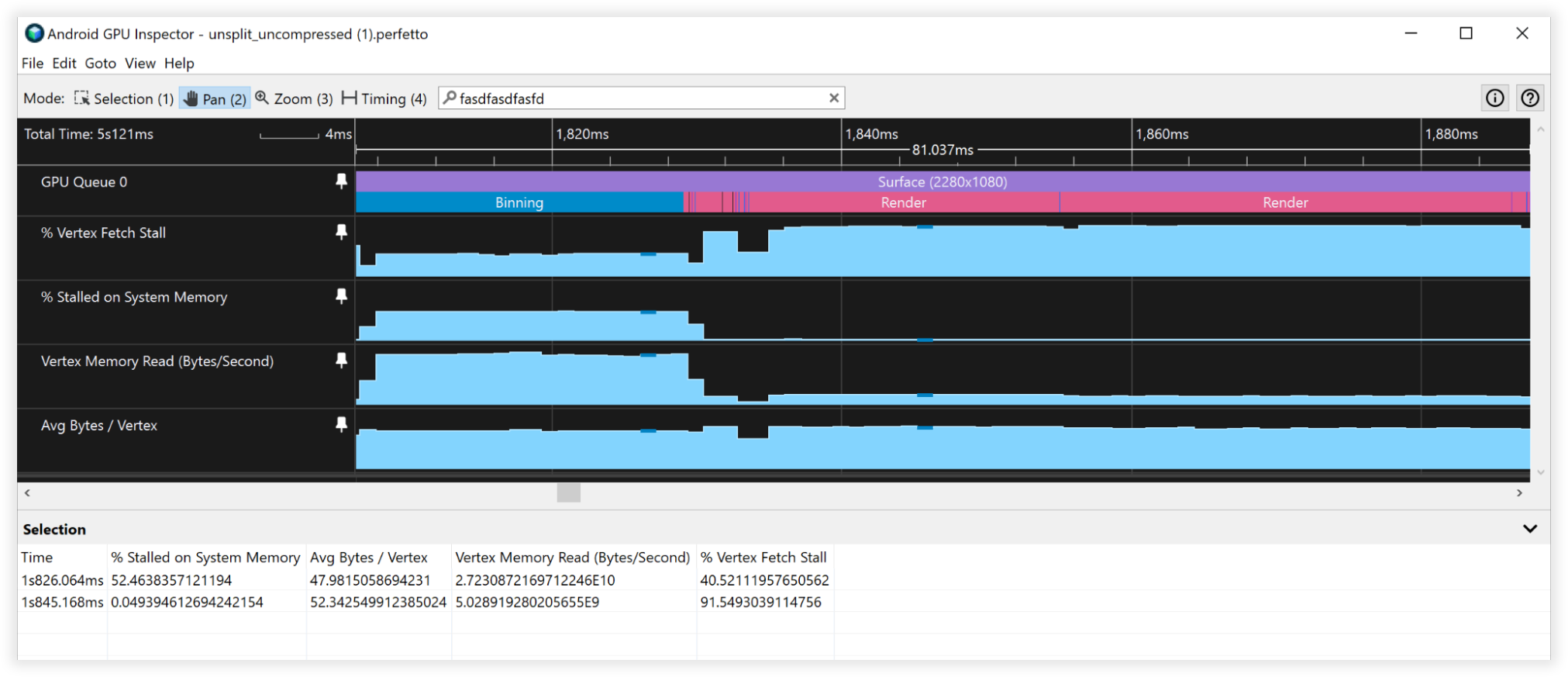
شکل 3: نمای بازرس GPU Android از رئوس فشرده نشده
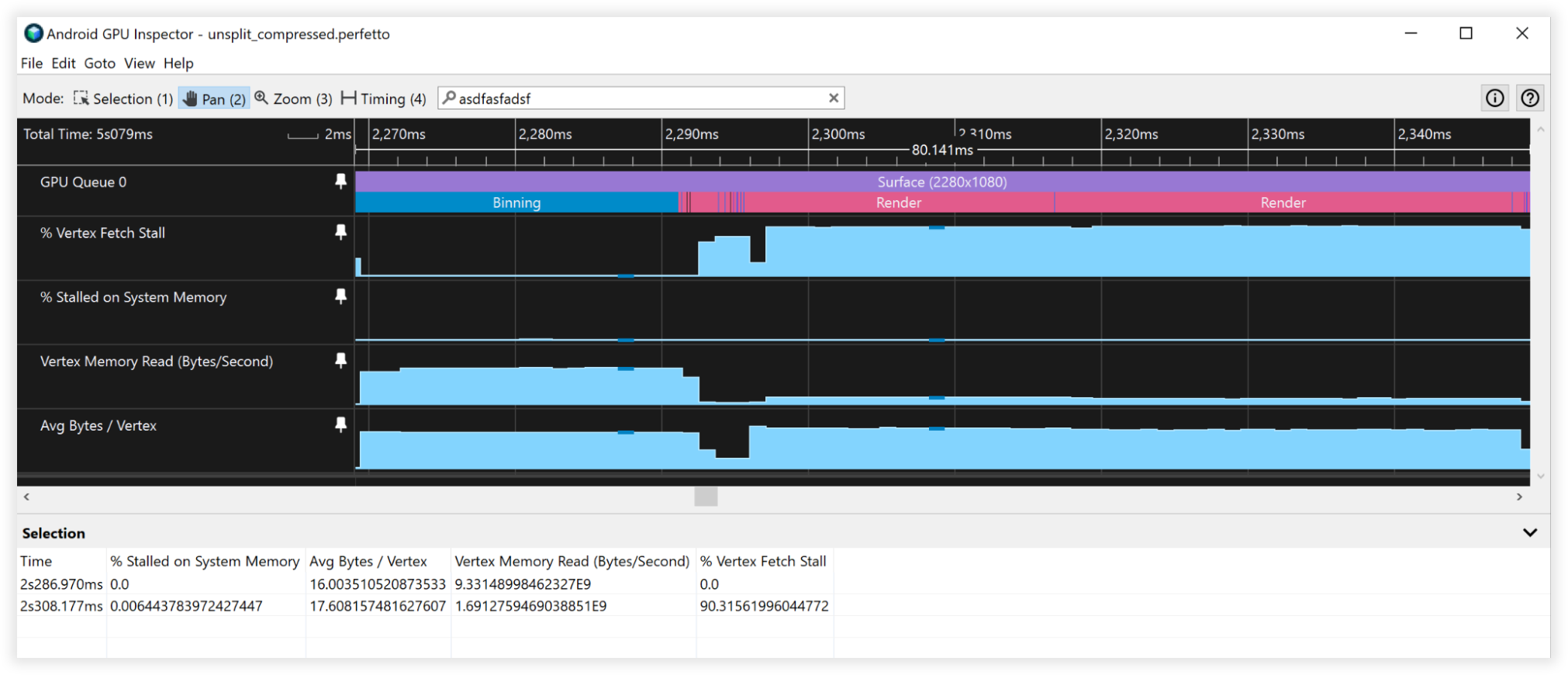
شکل 4: نمای بازرس GPU Android از رئوس فشرده
تقسیم جریان راس
Vertex Stream Splitting سازماندهی داده ها را در بافر رأس بهینه می کند. این یک بهینهسازی عملکرد حافظه نهان است که در GPUهای مبتنی بر کاشی که معمولاً در دستگاههای Android یافت میشوند تفاوت ایجاد میکند - به ویژه در مرحله binning فرآیند رندر.
پردازندههای گرافیکی مبتنی بر کاشی، سایهزنی ایجاد میکنند که مختصات نرمال شده دستگاه را بر اساس سایهزن راس ارائهشده برای انجام binning محاسبه میکند. ابتدا روی هر رأس صحنه اجرا می شود، چه قابل مشاهده باشد و چه نباشد. بنابراین، پیوسته نگه داشتن داده های موقعیت راس در حافظه یک مزیت بزرگ است. مکانهای دیگری که این طرحبندی جریان راس میتواند مفید باشد، برای پاسهای سایه است، زیرا معمولاً فقط به دادههای موقعیت برای محاسبات سایهها و همچنین پیشگذرهای عمق نیاز دارید، که تکنیکی است که معمولاً برای رندرینگ کنسول/رومیزی استفاده میشود. این طرح جریان راس می تواند یک پیروزی برای چندین کلاس موتور رندر باشد!
تقسیم جریان شامل تنظیم بافر راس با یک بخش به هم پیوسته از داده های موقعیت راس و یک بخش دیگر حاوی ویژگی های رأس به هم پیوسته است. اکثر برنامه ها معمولاً بافرهای خود را با درهم آمیختن کامل همه ویژگی ها تنظیم می کنند. این تصویر تفاوت را توضیح می دهد:
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
نگاهی به نحوه واکشی دادههای راس توسط GPU به ما کمک میکند تا مزایای تقسیم جریان را درک کنیم. برای استدلال فرض کنید:
- خطوط کش 32 بایتی (اندازه بسیار رایج)
- فرمت Vertex شامل:
- موقعیت، vec3<float32> = 12 بایت
- vec3 معمولی<float32> = 12 بایت
- مختصات UV vec2<float32> = 8 بایت
- حجم کل = 32 بایت
هنگامی که GPU دادهها را برای binning از حافظه واکشی میکند، یک خط کش 32 بایتی برای کار کردن میکشد. بدون تقسیم جریان راس، در واقع فقط از 12 بایت اول این خط کش برای binning استفاده می کند و 20 بایت دیگر را هنگام واکشی راس بعدی دور می اندازد. با تقسیم جریان راس، موقعیتهای راس در حافظه به هم پیوسته خواهند بود، بنابراین وقتی آن قطعه 32 بایتی به حافظه پنهان کشیده میشود، در واقع شامل 2 موقعیت رأس کامل برای عمل کردن قبل از بازگشت به حافظه اصلی برای واکشی بیشتر خواهد بود. 2 برابر بهبود!
حال، اگر تقسیم جریان راس را با فشرده سازی راس ترکیب کنیم، اندازه یک موقعیت راس منفرد را به 6 بایت کاهش می دهیم، بنابراین یک خط کش 32 بایتی که از حافظه سیستم کشیده می شود، 5 موقعیت راس کامل برای کار کردن دارد. بهبود 5 برابری!
نتایج تقسیم جریان راس
- پهنای باند خواندن حافظه Vertex:
- Binning: 27GB/s تا 6.5GB/s
- رندر: 4.5GB/s تا 4.5GB/s
- استالهای واکشی Vertex:
- باینینگ: 40% تا 0%
- رندر: 90% تا 90%
- میانگین بایت/راس:
- Binning: 48B تا 12B
- رندر: 52B تا 52B

شکل 5: نمای بازرس GPU Android از جریان های راس تقسیم نشده
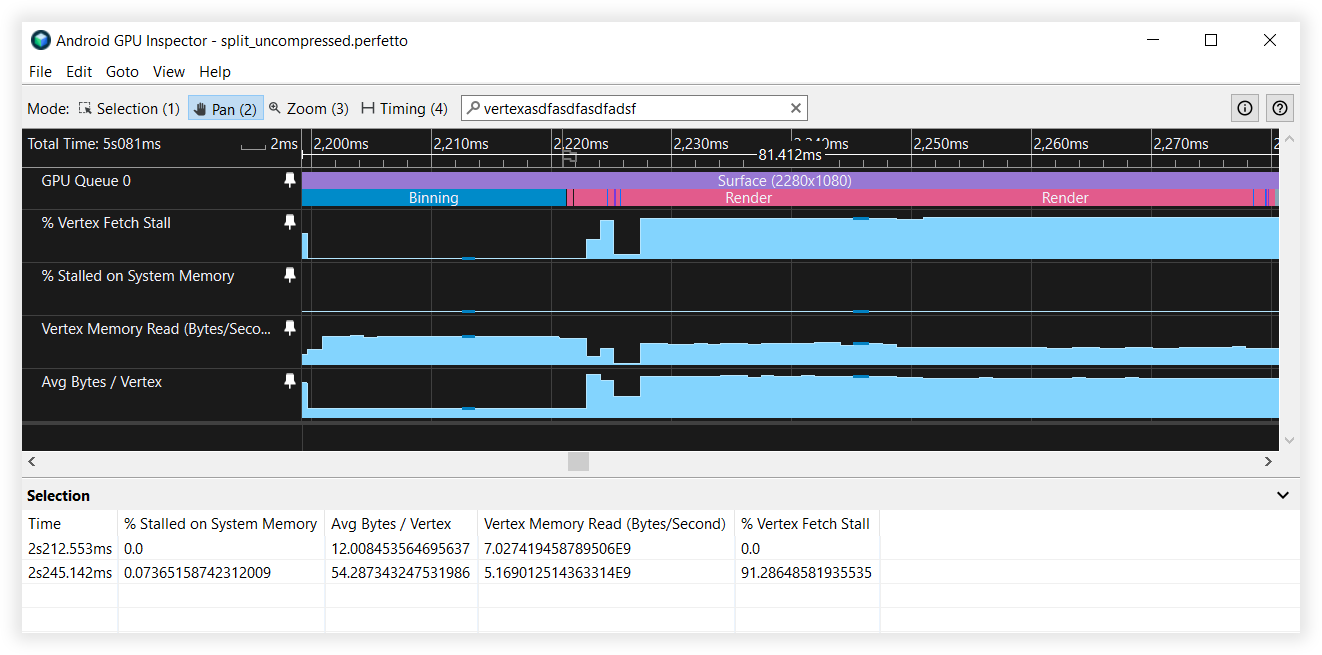
شکل 6: نمای بازرس GPU Android از جریان های راس تقسیم شده
نتایج ترکیبی
- پهنای باند خواندن حافظه Vertex:
- Binning: 25GB/s تا 4.5GB/s
- رندر: 4.5GB/s تا 1.7GB/s
- استالهای واکشی Vertex:
- باینینگ: 41% تا 0%
- رندر: 90% تا 90%
- میانگین بایت/راس:
- Binning: 48B تا 8B
- رندر: 52B تا 19B

شکل 7: نمای بازرس GPU Android از جریان های راس غیرفشرده و فشرده نشده
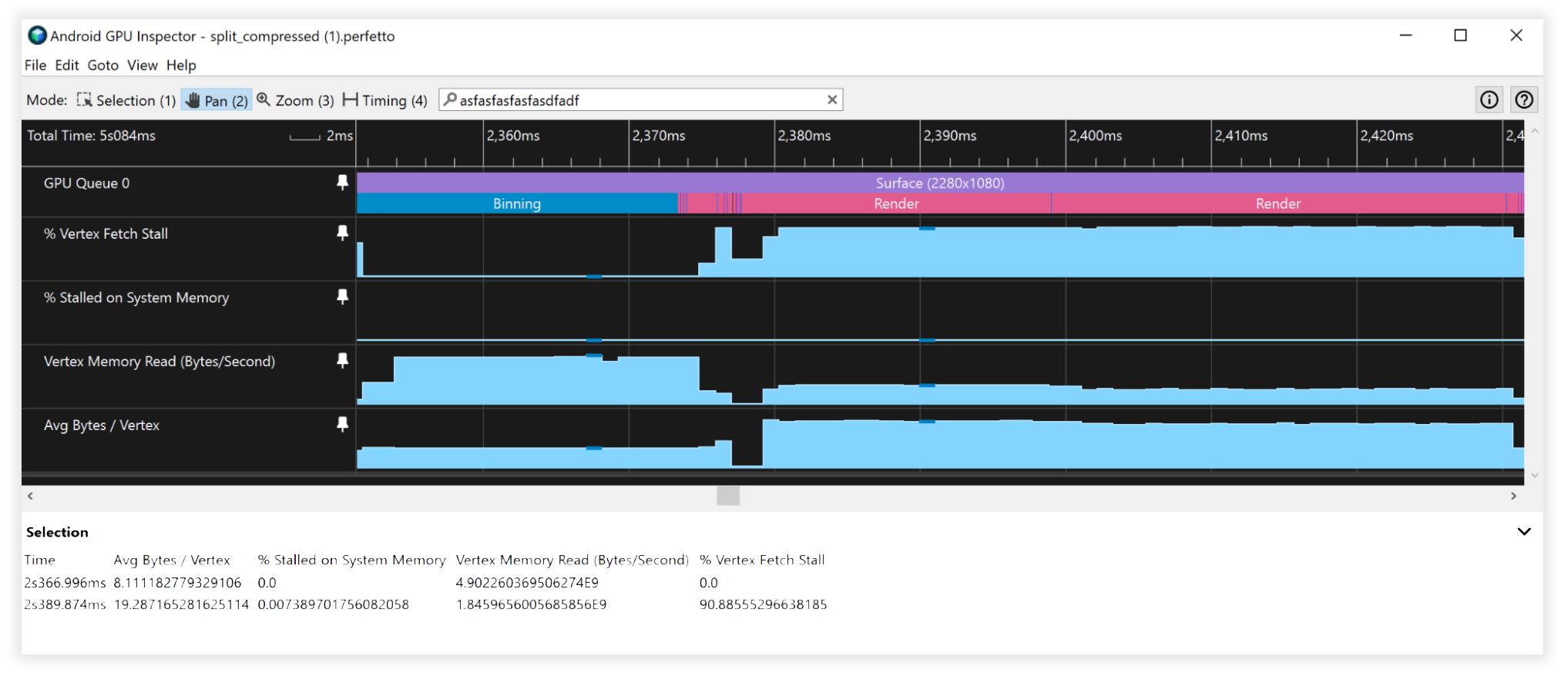
شکل 8: نمای بازرس GPU Android از جریان های راس فشرده و تقسیم شده
ملاحظات اضافی
داده بافر شاخص 16 در مقابل 32 بیتی
- مش ها را همیشه تقسیم/تکه کنید تا در یک بافر شاخص 16 بیتی (حداکثر 65536 راس منحصر به فرد) قرار گیرند. این به رندر نمایهشده در موبایل کمک میکند، زیرا واکشی دادههای راس ارزانتر است و انرژی کمتری مصرف میکند.
فرمتهای ویژگی بافر Vertex پشتیبانینشده
- فرمتهای راس SSCALED به طور گسترده در تلفن همراه پشتیبانی نمیشوند، و زمانی که استفاده میشوند میتوانند در درایورهایی که سعی میکنند در صورت نداشتن پشتیبانی سختافزاری از آنها تقلید کنند، عملکرد پرهزینهای را به همراه داشته باشد. همیشه به سراغ SNORM بروید و هزینه ناچیز ALU را برای فشرده سازی بپردازید.


