Хорошее расположение и сжатие данных вершин является неотъемлемой частью производительности любого графического приложения, независимо от того, состоит ли оно из двухмерных пользовательских интерфейсов или представляет собой большую трехмерную игру с открытым миром. Внутреннее тестирование с помощью Frame Profiler Android GPU Inspector на десятках лучших игр для Android показывает, что можно многое сделать для улучшения управления данными вершин. Мы заметили, что для данных вершин обычно используются 32-битные значения с плавающей запятой полной точности для всех атрибутов вершин и макет буфера вершин, который использует массив структур, отформатированных с полностью чередующимися атрибутами.
В этой статье обсуждается, как оптимизировать графическую производительность вашего приложения Android, используя следующие методы:
- Сжатие вершин
- Разделение потока вершин
Реализация этих методов может улучшить использование пропускной способности вершинной памяти до 50 %, уменьшить конфликты между шиной памяти и ЦП, уменьшить задержки системной памяти и увеличить время автономной работы; все это является победой как для разработчиков, так и для конечных пользователей!
Все представленные данные взяты из примера статической сцены, содержащей около 19 000 000 вершин, запущенной на Pixel 4:

Рисунок 1. Пример сцены с 6 кольцами и 19-метровыми вершинами.
Сжатие вершин
Сжатие вершин — это общий термин для методов сжатия с потерями, которые используют эффективную упаковку для уменьшения размера данных вершин как во время выполнения, так и при хранении. Уменьшение размера вершин имеет несколько преимуществ, включая уменьшение пропускной способности памяти графического процессора (путем обмена вычислительных ресурсов на пропускную способность), улучшение использования кэша и потенциальное снижение риска переполнения регистров.
Общие подходы к сжатию вершин включают в себя:
- Уменьшение числовой точности атрибутов данных вершин (например, с 32-битного числа с плавающей запятой на 16-битное с плавающей запятой)
- Представление атрибутов в разных форматах
Например, если вершина использует полные 32-битные числа с плавающей запятой для положения (vec3), нормали (vec3) и координат текстуры (vec2), замена всех этих чисел на 16-битные числа с плавающей запятой уменьшит размер вершины на 50 % (16 байт на средняя вершина размером 32 байта).
Позиции вершин
Данные о положении вершин могут быть сжаты от 32-битных значений с плавающей запятой полной точности до 16-битных значений с плавающей запятой половинной точности в подавляющем большинстве сеток, а половинные числа с плавающей запятой поддерживаются аппаратно почти на всех мобильных устройствах. Функция преобразования, переходящая из float32 в float16, выглядит следующим образом ( адаптировано из этого руководства ):
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
У этого подхода есть ограничение; Точность ухудшается по мере удаления вершины от начала координат, что делает ее менее подходящей для сеток, которые имеют очень большие пространственные размеры (вершины, имеющие элементы, выходящие за пределы 1024). Вы можете решить эту проблему, разбив сетку на более мелкие фрагменты, центрируя каждый фрагмент вокруг начала координат модели и масштабируя его так, чтобы все вершины каждого фрагмента помещались в диапазон [-1, 1], который содержит наивысшую точность для чисел с плавающей запятой. ценности. Псевдокод сжатия выглядит следующим образом:
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
Вы запекаете масштабный коэффициент и переводите его в матрицу модели, чтобы распаковать данные вершин при рендеринге. Имейте в виду, что вы не хотите использовать одну и ту же модельную матрицу для преобразования нормалей, поскольку к ним не применялось одинаковое сжатие. Вам понадобится матрица без этих преобразований декомпрессии для нормалей или вы можете использовать матрицу базовой модели (которую можно использовать для нормалей), а затем применить дополнительные преобразования декомпрессии к матрице модели в шейдере. Пример:
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
Другой подход предполагает использование нормализованных целых чисел со знаком (SNORM) . Типы данных SNORM используют целые числа, а не плавающую точку для представления значений между [-1, 1]. Использование 16-битного SNORM для позиций дает такую же экономию памяти, как и float16, без недостатков неравномерного распределения. Реализация, которую мы рекомендуем для использования SNORM, выглядит следующим образом:
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| Формат | Размер | |
|---|---|---|
| До | vec4< float32 > | 16 байт |
| После | vec3< float16/SNORM16 > | 6 байт |
Нормали вершин и касательное пространство
Вершинные нормали необходимы для освещения, а касательное пространство необходимо для более сложных методов, таких как наложение нормалей.
Касательное пространство
Касательное пространство — это система координат, в которой каждая вершина состоит из вектора нормали, касательной и бикасательной. Поскольку эти три вектора обычно ортогональны друг другу, нам нужно сохранить только два из них, а третий можно вычислить, взяв векторное произведение двух других в вершинном шейдере.
Эти векторы обычно могут быть представлены с использованием 16-битных чисел с плавающей запятой без каких-либо потерь в визуальной точности, так что это хорошее место для начала!
Мы можем сжать дальше с помощью метода, известного как QTangents, который сохраняет все касательное пространство в одном кватернионе. Поскольку кватернионы можно использовать для представления вращения, думая о векторах касательного пространства как о векторах-столбцах матрицы 3x3, представляющей вращение (в данном случае из пространства модели в касательное пространство), мы можем конвертировать между ними! Кватернион можно рассматривать как vec4 с точки зрения данных, а преобразование векторов касательного пространства в QTangent на основе статьи, указанной выше и адаптированной из реализации здесь, выглядит следующим образом:
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
Кватернион будет нормализован, и вы сможете сжать его с помощью SNORM. 16-битные SNORM обеспечивают хорошую точность и экономию памяти. 8-битные SNORM могут обеспечить еще большую экономию, но могут вызвать артефакты на сильнозеркальных материалах. Вы можете попробовать оба и посмотреть, что лучше всего подходит для ваших активов! Кодирование кватерниона выглядит следующим образом:
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
Чтобы декодировать кватернион в вершинном шейдере ( адаптировано отсюда ):
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| Формат | Размер | |
|---|---|---|
| До | vec3< float32 > + vec3< float32 > + vec3< float32 > | 36 байт |
| После | vec4< SNORM16 > | 8 байт |
Только нормальные люди
Если вам нужно хранить только векторы нормалей, существует другой подход, который может привести к большей экономии — использование октаэдрического отображения единичных векторов, а не декартовых координат для сжатия вектора нормали . Октаэдральное картографирование работает путем проецирования единичной сферы на октаэдр, а затем проецирования октаэдра на двумерную плоскость. В результате вы можете представить любой нормальный вектор, используя всего два числа. Эти два числа можно рассматривать как координаты текстуры, которые мы используем для «выборки» 2D-плоскости, на которую мы проецировали сферу, что позволяет нам восстановить исходный вектор. Эти два числа затем можно сохранить в SNORM8.
Рисунок 2. Визуализация октаэдрического отображения ( источник )
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
Распаковка в вершинном шейдере (для преобразования обратно в декартовы координаты) обходится недорого; на большинстве современных мобильных устройств мы не заметили какого-либо значительного снижения производительности при реализации этого метода. Распаковка в вершинном шейдере:
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
Этот подход также можно использовать для хранения всего касательного пространства, используя этот метод для хранения векторов нормали и касательной с помощью vec2 SNORM8 , но вам нужно будет найти способ сохранить направление битангенса (необходимо для общего сценария, когда у вас есть зеркальные UV-координаты на модели). Один из способов реализовать это — отобразить компонент кодировки касательного вектора так, чтобы он всегда был положительным, а затем перевернуть его знак, если вам нужно перевернуть направление касательной, и проверить это в вершинном шейдере:
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| Формат | Размер | |
|---|---|---|
| До | vec3< float32 > | 12 байт |
| После | vec2< SNORM8 > | 2 байта |
UV-координаты вершин
UV-координаты, используемые для наложения текстур (помимо прочего), обычно хранятся с использованием 32-битных чисел с плавающей запятой. Сжатие их с помощью 16-битных чисел с плавающей запятой вызывает проблемы с точностью для текстур размером более 1024x1024; Точность с плавающей запятой между [0,5, 1,0] означает, что значения будут увеличиваться более чем на 1 пиксель!
Лучшим подходом является использование беззнаковых нормализованных целых чисел (UNORM), в частности UNORM16; это обеспечивает равномерное распределение по всему диапазону координат текстуры, поддерживая текстуры размером до 65536x65536! Предполагается, что координаты текстуры находятся в диапазоне [0,0, 1,0] для каждого элемента, что может быть не так в зависимости от сетки (например, стены могут использовать координаты текстуры, выходящие за пределы 1,0), поэтому имейте это в виду при рассмотрении этой техники. . Функция преобразования будет выглядеть так:
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| Формат | Размер | |
|---|---|---|
| До | vec2< float32 > | 8 байт |
| После | vec2< UNORM16 > | 4 байта |
Результаты сжатия вершин
Эти методы сжатия вершин привели к сокращению объема памяти вершин на 66%: с 48 байт до 16 байт. Это проявлялось как:
- Пропускная способность чтения памяти вершин:
- Биннинг: от 27 ГБ/с до 9 ГБ/с
- Рендеринг: от 4,5 Б/с до 1,5 ГБ/с.
- Остановки выборки вершин:
- Биннинг: от 50% до 0%
- Рендеринг: от 90% до 90%
- Среднее количество байт/вершина:
- Биннинг: от 48B до 16B
- Рендеринг: от 52B до 18B
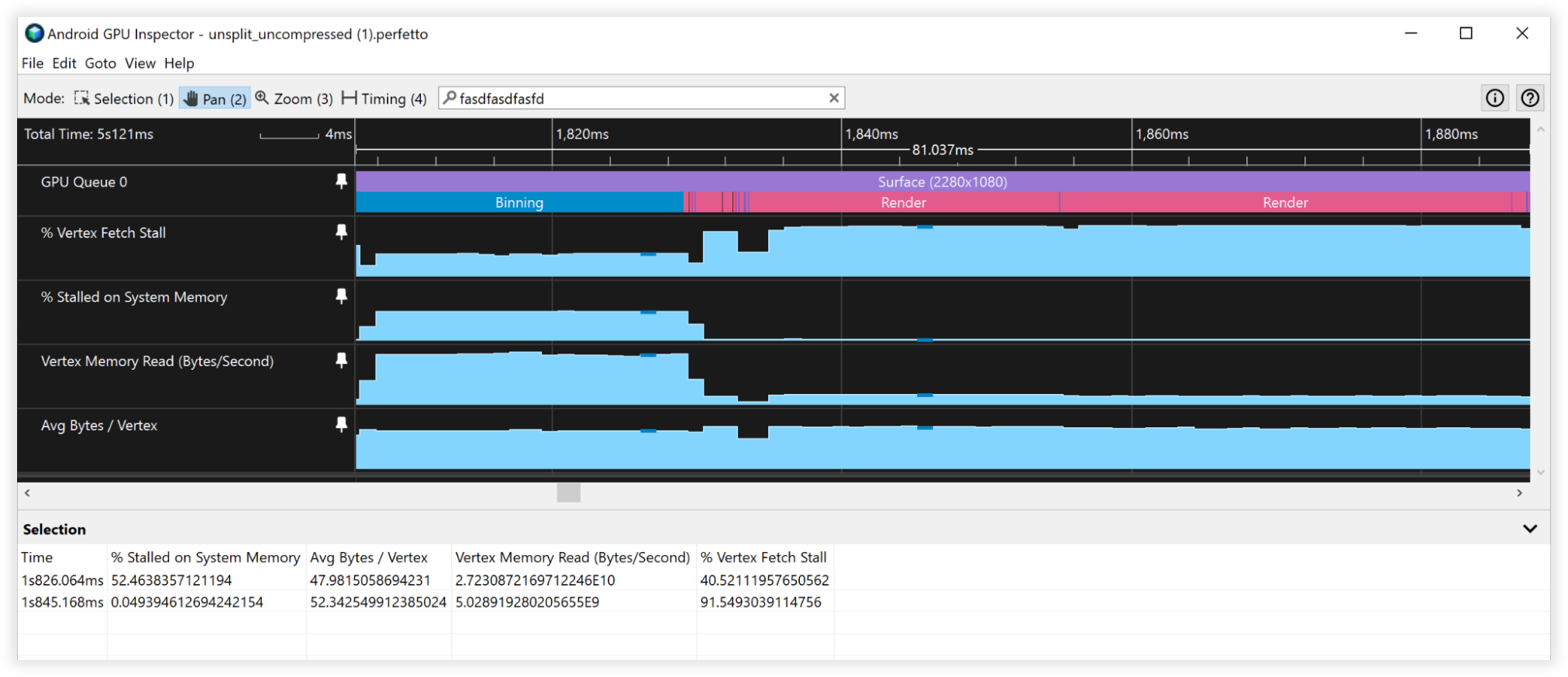
Рис. 3. Представление несжатых вершин в Android GPU Inspector
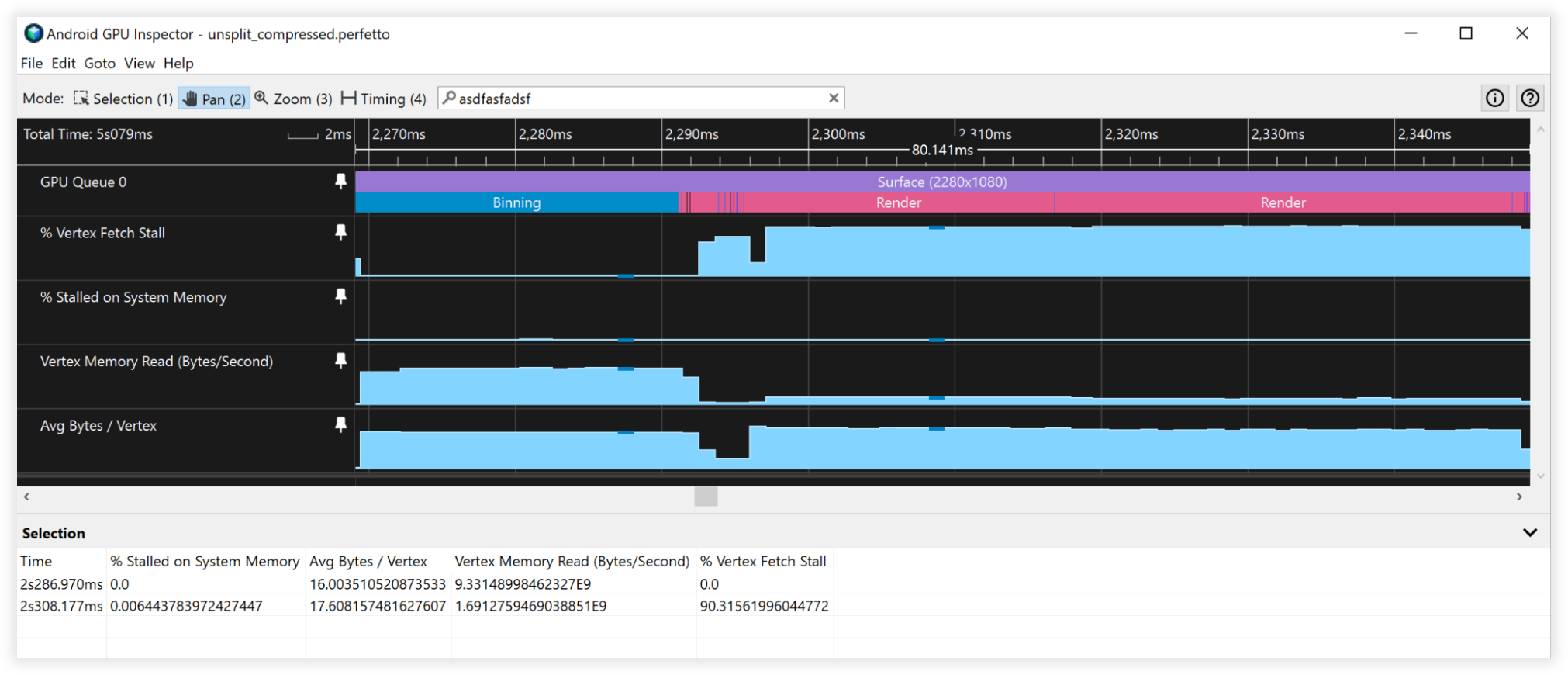
Рис. 4. Вид сжатых вершин в Android GPU Inspector.
Разделение потока вершин
Разделение потока вершин оптимизирует организацию данных в буфере вершин. Это оптимизация производительности кэша, которая имеет значение для графических процессоров на основе плиток, обычно встречающихся в устройствах Android, особенно на этапе объединения в процессе рендеринга.
Графические процессоры на основе плиток создают шейдер, который вычисляет нормализованные координаты устройства на основе предоставленного вершинного шейдера для выполнения биннинга. Сначала он выполняется для каждой вершины сцены, независимо от того, видима она или нет. Поэтому сохранение данных о положении вершин в памяти является большим плюсом. Другие места, где макет потока вершин может быть полезен, — это проходы теней, поскольку обычно вам нужны только данные о положении для вычислений теней, а также предварительные проходы глубины, которые обычно используются для рендеринга консоли/рабочего стола; такая компоновка потока вершин может оказаться выигрышной для нескольких классов движка рендеринга!
Разделение потока включает в себя настройку буфера вершин с непрерывным разделом данных о положении вершин и другим разделом, содержащим чередующиеся атрибуты вершин. Большинство приложений обычно настраивают свои буферы, полностью чередуя все атрибуты. Это изображение объясняет разницу:
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
Изучение того, как графический процессор извлекает данные вершин, помогает нам понять преимущества разделения потока. Предположим ради аргументации:
- 32-байтовые строки кэша (довольно распространенный размер)
- Формат вершин, состоящий из:
- Позиция, vec3<float32> = 12 байт
- Обычный vec3<float32> = 12 байт
- UV-координаты vec2<float32> = 8 байт
- Общий размер = 32 байта.
Когда графический процессор извлекает данные из памяти для объединения, он извлекает для работы 32-байтовую строку кэша. Без разделения потока вершин он фактически будет использовать только первые 12 байтов этой строки кэша для объединения и отбрасывать остальные 20 байтов при выборке следующей вершины. При разделении потока вершин позиции вершин будут в памяти непрерывными, поэтому, когда этот 32-байтовый фрагмент будет помещен в кэш, он фактически будет содержать две целые позиции вершин, над которыми нужно будет работать, прежде чем придется возвращаться в основную память для получения большего количества. Улучшение в 2 раза!
Теперь, если мы объединим разделение потока вершин со сжатием вершин, мы уменьшим размер одной позиции вершины до 6 байт, поэтому одна 32-байтовая строка кэша, извлеченная из системной памяти, будет иметь 5 полных позиций вершин для работы: улучшение в 5 раз!
Результаты разделения потока вершин
- Пропускная способность чтения памяти вершин:
- Биннинг: от 27 ГБ/с до 6,5 ГБ/с
- Рендеринг: от 4,5 ГБ/с до 4,5 ГБ/с.
- Остановки выборки вершин:
- Биннинг: от 40% до 0%
- Рендеринг: от 90% до 90%
- Среднее количество байт/вершина:
- Биннинг: от 48B до 12B
- Рендеринг: от 52B до 52B

Рис. 5. Представление Android GPU Inspector неразделенных потоков вершин
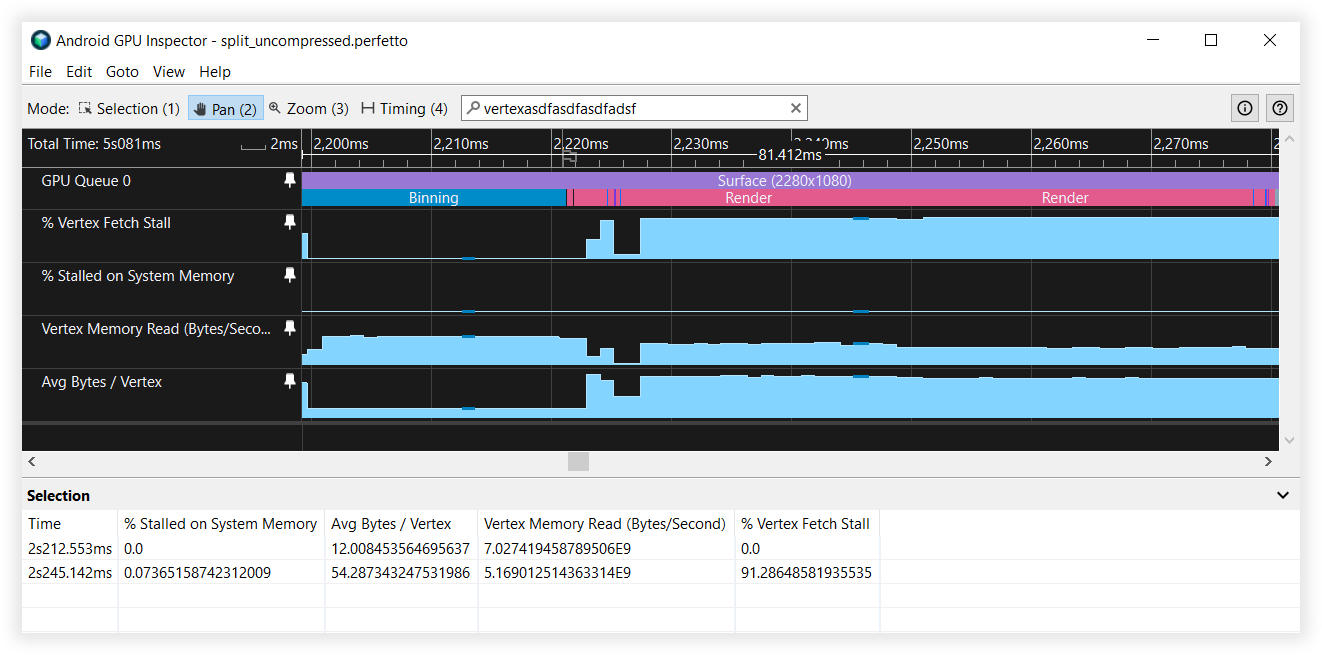
Рис. 6. Вид разделенных потоков вершин в Android GPU Inspector.
Сложные результаты
- Пропускная способность чтения памяти вершин:
- Биннинг: от 25 ГБ/с до 4,5 ГБ/с.
- Рендеринг: от 4,5 ГБ/с до 1,7 ГБ/с.
- Остановки выборки вершин:
- Биннинг: от 41% до 0%
- Рендеринг: от 90% до 90%
- Среднее количество байт/вершина:
- Биннинг: от 48B до 8B
- Рендеринг: от 52B до 19B.

Рис. 7. Представление Android GPU Inspector с неразделенными несжатыми потоками вершин.
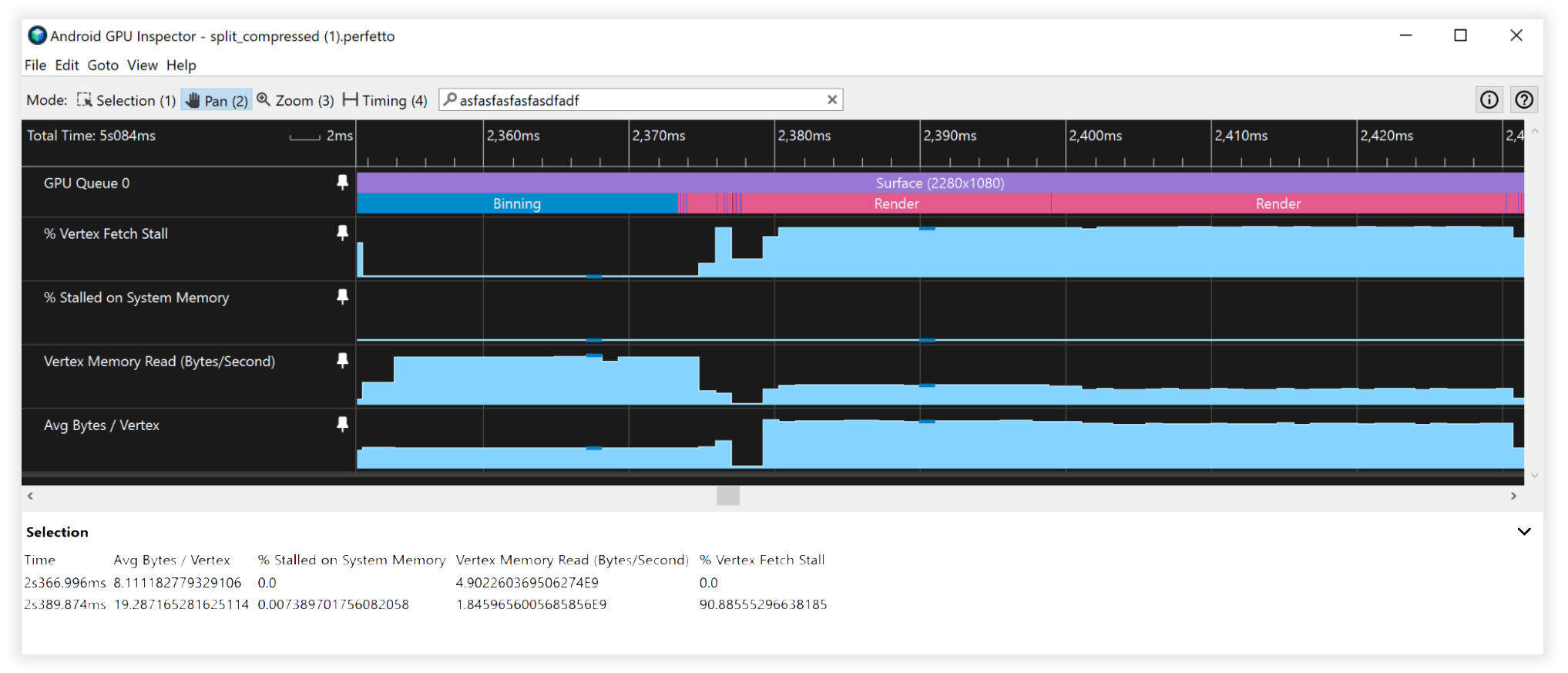
Рис. 8. Представление Android GPU Inspector разделенных сжатых потоков вершин.
Дополнительные соображения
16- и 32-битные данные индексного буфера
- Всегда разделяйте/разбивайте сетки так, чтобы они помещались в 16-битный индексный буфер (максимум 65536 уникальных вершин). Это поможет при индексированном рендеринге на мобильных устройствах, поскольку получение данных вершин обходится дешевле и потребляется меньше энергии.
Неподдерживаемые форматы атрибутов буфера вершин
- Форматы вершин SSCALED не получили широкой поддержки на мобильных устройствах, и при их использовании могут возникнуть дорогостоящие потери производительности в драйверах, которые пытаются их эмулировать, если у них нет аппаратной поддержки. Всегда выбирайте SNORM и платите незначительную стоимость ALU для распаковки.


