การจัดการข้อมูล Vertex

การจัดวางและการบีบอัดข้อมูล Vertex ที่ดีเป็นส่วนสำคัญมากต่อประสิทธิภาพของแอปพลิเคชันแบบกราฟิก ไม่ว่าแอปจะประกอบไปด้วยอินเทอร์เฟซผู้ใช้แบบ 2 มิติหรือจะเป็นเกมโอเพนเวิลด์ 3 มิติขนาดใหญ่ก็ตาม การทดสอบภายในกับ Frame Profiler ของ Android GPU กับเกม Android ยอดนิยมหลายสิบเกมชี้ให้เห็นว่าสามารถทำอะไรได้บ้างเพื่อปรับปรุงการจัดการข้อมูล Vertex เราสังเกตเห็นว่าเป็นเรื่องปกติที่ข้อมูล Vertex จะใช้ความแม่นยําแบบเต็ม ค่าจำนวนลอยตัว 32 บิตสำหรับแอตทริบิวต์ Vertex ทั้งหมด และรูปแบบบัฟเฟอร์ของ Vertex ที่ใช้อาร์เรย์ของโครงสร้างที่มีการจัดรูปแบบด้วยแอตทริบิวต์ที่มีการแทรกสลับแบบเต็ม

บทความนี้อธิบายวิธีการเพิ่มประสิทธิภาพกราฟิกของแอปพลิเคชัน Android โดยใช้เทคนิคต่อไปนี้

• การบีบอัด Vertex
• การแยกสตรีม Vertex

การใช้เทคนิคเหล่านี้จะช่วยเพิ่มการใช้งานแบนด์วิดท์หน่วยความจำของ Vertex ได้ถึง 50% ลดการช่วงชิงบัสหน่วยความจำกับ CPU ลดการค้างในหน่วยความจำของระบบ และปรับปรุงอายุแบตเตอรี่ ซึ่งล้วนแล้วแต่ประสบความสำเร็จทั้งสำหรับนักพัฒนาแอปและผู้ใช้ปลายทาง

ข้อมูลทั้งหมดที่แสดงมาจากตัวอย่างฉากนิ่งที่มีจุดยอดประมาณ 19,000,000 จุดที่ทำงานใน Pixel 4

รูป 1: ตัวอย่างฉากที่มีวงแหวน 6 วงและยอดแหลมยาว 19 เมตร

การบีบอัด Vertex

Vertex Compression เป็นคำรวมที่ใช้เรียกเทคนิคการบีบอัดแบบสูญเสียบางส่วนที่ ใช้การบรรจุอย่างมีประสิทธิภาพเพื่อลดขนาดข้อมูล Vertex ทั้งระหว่างรันไทม์และพื้นที่เก็บข้อมูล การลดขนาดของจุดยอดมีประโยชน์หลายประการ รวมถึงการลดแบนด์วิดท์ของหน่วยความจำใน GPU (โดยการซื้อขายค่าแบนด์วิดท์) การปรับปรุงการใช้งานแคช และอาจลดความเสี่ยงของการลงทะเบียนที่รั่วไหล

วิธีทั่วไปในการบีบอัด Vertex ได้แก่

• ลดความแม่นยำของตัวเลขของแอตทริบิวต์ข้อมูล Vertex (เช่น ทศนิยม 32 บิตเป็นทศนิยม 16 บิต)
• นำเสนอแอตทริบิวต์ในรูปแบบต่างๆ

ตัวอย่างเช่น หาก Vertex ใช้ Float 32 บิตแบบเต็มสำหรับตำแหน่ง (vec3), ปกติ (vec3) และพิกัดพื้นผิว (vec2) การแทนที่ทั้งหมดนี้ด้วยทศนิยม 16 บิตจะลดขนาด Vertex ลง 50% (16 ไบต์ใน Vertex 32 ไบต์โดยเฉลี่ย)

ตำแหน่งจุดยอดมุม

ข้อมูลตำแหน่ง Vertex สามารถบีบอัดจากค่าจุดลอยตัว 32 บิตที่มีความแม่นยำเต็มรูปแบบ เป็นค่าจุดลอยตัว 16 บิตที่มีความแม่นยำครึ่งหนึ่งใน Mesh ส่วนใหญ่ และครึ่ง Float ได้รับการสนับสนุนในฮาร์ดแวร์ในอุปกรณ์เคลื่อนที่เกือบทุกรุ่น ฟังก์ชัน Conversion ที่เปลี่ยนจาก Float32 ไป Float 16 มีลักษณะดังนี้ (ดัดแปลงมาจากคู่มือนี้)

uint16_t f32_to_f16(float f) {
  uint32_t x = (uint32_t)f;
  uint32_t sign = (unsigned short)(x >> 31);
  uint32_t mantissa;
  uint32_t exp;
  uint16_t hf;

  mantissa = x & ((1 << 23) - 1);
  exp = x & (0xFF << 23);
  if (exp >= 0x47800000) {
    // check if the original number is a NaN
    if (mantissa && (exp == (0xFF << 23))) {
      // single precision NaN
      mantissa = (1 << 23) - 1;
    } else {
      // half-float will be Inf
      mantissa = 0;
    }
    hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
         (uint16_t)(mantissa >> 13);
  }
  // check if exponent is <= -15
  else if (exp <= 0x38000000) {
    hf = 0;  // too small to be represented
  } else {
    hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
         (uint16_t)(mantissa >> 13);
  }

  return hf;
}

แนวทางนี้มีข้อจำกัด ความแม่นยําจะลดลงเมื่อจุดยอดมุมอยู่ไกลจากต้นทาง ทำให้ไม่เหมาะกับโครงข่ายซึ่งมีพื้นที่ที่มีขนาดใหญ่มาก (จุดยอดที่มีองค์ประกอบเกิน 1024) คุณแก้ไขปัญหานี้ได้โดยแบ่งตาข่ายออกเป็นส่วนเล็กๆ จัดส่วนเล็กๆ ให้อยู่กึ่งกลางรอบๆ ต้นทางของโมเดล และใช้การปรับขนาดเพื่อให้จุดยอดทั้งหมดของแต่ละส่วนพอดีกับช่วง [-1, 1] ซึ่งมีความแม่นยำสูงสุดสำหรับค่าจุดลอยตัว Pseudocode สำหรับการบีบอัดจะมีลักษณะดังนี้

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));

คุณอบค่าตัวคูณมาตราส่วนและการแปลลงในเมทริกซ์โมเดลเพื่อคลายการบีบอัดข้อมูลจุดยอดมุมเมื่อแสดงผล โปรดทราบว่าคุณไม่ต้องการใช้เมทริกซ์โมเดลเดียวกันนี้ในการแปลงค่าปกติ เนื่องจากไม่ได้บีบอัดแบบเท่ากัน คุณจะต้องใช้เมทริกซ์ที่ไม่มีการแปลงการขยายข้อมูลที่บีบอัดเหล่านี้สำหรับค่าปกติ หรือใช้เมทริกซ์โมเดลฐาน (ซึ่งคุณใช้สำหรับปกติได้) แล้วใช้การแปลงการลดการบีบอัดเพิ่มเติมกับเมทริกซ์โมเดลภายในตัวปรับแสงเงา ตัวอย่าง

vec3 in in_pos;

void main() {
   ...
   // bounding box data packed into uniform buffer
   vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
   gl_Position = proj * view * model * decompress_pos;
}

อีกวิธีหนึ่งคือการใช้จำนวนเต็มปกติที่ลงนาม (SNORM) ประเภทข้อมูล SNORM ใช้จำนวนเต็มแทนจุดลอยตัวเพื่อแสดงค่าระหว่าง [-1, 1] การใช้ SNORM แบบ 16 บิตสำหรับตำแหน่งต่างๆ จะช่วยให้คุณประหยัดหน่วยความจำได้เท่ากับ Float 16 โดยไม่มีข้อเสียของการกระจายที่ไม่สม่ำเสมอ การดำเนินการที่เราแนะนำให้ใช้กับ SNORM มีลักษณะดังนี้

const int BITS = 16

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   // float to integer value conversion
   p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1) 

	รูปแบบ	ขนาด
ก่อน	vec4<float32>	16 ไบต์
หลัง	vec3<float16/SNORM16>	6 ไบต์

จุดยอดมุมปกติและช่องว่างแทนเจนต์

จำเป็นต้องใช้ Vertex ปกติสำหรับการจัดแสง และต้องมีพื้นที่แทนเจนต์สำหรับเทคนิคที่ซับซ้อนมากขึ้น เช่น การแมปปกติ

ปริภูมิแทน

ปริภูมิแทนเจนต์เป็นระบบพิกัดที่ทุกจุดยอดประกอบด้วยเวกเตอร์ปกติ แทนเจนต์ และบิตเทนเจนต์ เนื่องจากเวกเตอร์ทั้ง 3 นี้มักจะเป็นแนวฉากตรงข้ามกัน เราจึงต้องจัดเก็บเวกเตอร์ไว้เพียง 2 เวกเตอร์ และช่วยคำนวณหาเวกเตอร์ที่ 3 ได้โดยการนำผลคูณไขว้ของอีก 2 เวกเตอร์ในตัวแสดงผล Vertex

โดยทั่วไปเวกเตอร์เหล่านี้สามารถแสดงโดยใช้การลอยตัว 16 บิตโดยไม่สูญเสียการรับรู้ในคุณภาพของภาพ จึงเป็นจุดที่ควรเริ่มต้น

เราสามารถบีบอัดเพิ่มเติมด้วยเทคนิคที่เรียกว่า QTangents ซึ่งเก็บพื้นที่แทนเจนต์ทั้งหมดไว้ในควอเทนเนียนเดียว เนื่องจากควอเทิร์นสามารถใช้เพื่อแสดงการหมุน โดยการคิดให้เวกเตอร์พื้นที่แทนเจนต์เป็นเวกเตอร์ของคอลัมน์ของเมทริกซ์ขนาด 3x3 ที่แสดงถึงการหมุน (ในกรณีนี้จากพื้นที่โมเดลลงในพื้นที่แทนเจนต์) เราจึงจะแปลงระหว่าง 2 ส่วนได้ ควอเทอร์เนียนอาจถือว่าเป็นข้อมูล vec4 และการแปลงจากเวกเตอร์พื้นที่แทนเจนต์เป็น QTangent โดยอิงจากเอกสารที่ลิงก์ด้านบน และปรับเปลี่ยนจากการติดตั้งใช้งานที่นี่มีดังนี้

const int BITS = 16

quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
   mat3 tbn = {normal, tangent, bitangent};
   quaternion qTangent(tbn);
   qTangent.normalize();

   //Make sure QTangent is always positive
   if (qTangent.w < 0)
       qTangent = -qTangent;

   const float bias = 1.0 / (2^(BITS - 1) - 1);

   //Because '-0' sign information is lost when using integers,
   //we need to apply a "bias"; while making sure the Quaternion
   //stays normalized.
   // ** Also our shaders assume qTangent.w is never 0. **
   if (qTangent.w < bias) {
       Real normFactor = Math::Sqrt( 1 - bias * bias );
       qTangent.w = bias;
       qTangent.x *= normFactor;
       qTangent.y *= normFactor;
       qTangent.z *= normFactor;
   }

   //If it's reflected, then make sure .w is negative.
   vec3 naturalBinormal = cross_product(tangent, normal);
   if (dot_product(naturalBinormal, binormal) <= 0)
       qTangent = -qTangent;
   return qTangent;
}

ระบบจะทำให้ควอเทอร์เนียนเป็นมาตรฐานและคุณจะบีบอัดได้โดยใช้ SNORM SNORM แบบ 16 บิตช่วยให้แม่นยำและประหยัดหน่วยความจำได้เป็นอย่างดี SNORM แบบ 8 บิตช่วยประหยัดได้มากกว่า แต่อาจทำให้มีอาร์ติแฟกต์ในวัสดุที่มีข้อมูลจำเพาะสูง คุณสามารถลองใช้ทั้ง 2 รูปแบบ แล้วดูว่าแบบใดเหมาะกับชิ้นงานของคุณที่สุด การเข้ารหัสควอเทอร์เนียนมีลักษณะดังนี้

for each vertex v in mesh:
   quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
   // Once we have the quaternion we can compress it
   res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);

วิธีถอดรหัสควอเทอร์เนียนในตัวปรับแสงเงา Vertex (ดัดแปลงจากที่นี่)

vec3 xAxis( vec4 qQuat )
{
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwy = fTy * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxy = fTy * qQuat.x;
  float fTxz = fTz * qQuat.x;
  float fTyy = fTy * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}

vec3 yAxis( vec4 qQuat )
{
  float fTx  = 2.0 * qQuat.x;
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwx = fTx * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxx = fTx * qQuat.x;
  float fTxy = fTy * qQuat.x;
  float fTyz = fTz * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}

void main() {
  vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
  vec3 normal = xAxis(qtangent);
  vec3 tangent = yAxis(qtangent);
  float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
  vec3 binormal = cross(normal, tangent) * biNormalReflection;
  ...
}

	รูปแบบ	ขนาด
ก่อน	vec3<float32> + vec3<float32> + vec3<float32>	36 ไบต์
หลัง	vec4<SNORM16>	8 ไบต์

ปกติเท่านั้น

หากคุณต้องการเก็บเฉพาะเวกเตอร์ปกติ มีวิธีอื่นที่สามารถช่วยให้คุณประหยัดได้ คือ การใช้การทำแผนที่ค่าเวกเตอร์ของหน่วยเวกเตอร์ แทนที่จะใช้พิกัดคาร์ทีเซียนเพื่อบีบอัดเวกเตอร์ปกติ การทำแผนที่ทรงแปดหน้าโดยฉายภาพทรงกลมหน่วยเป็นทรงแปดหน้า แล้วฉายภาพทรงแปดหน้าลงไปในระนาบ 2 มิติ ผลลัพธ์ก็คือ คุณสามารถแสดงเวกเตอร์ปกติใดๆ ได้โดยใช้ตัวเลขเพียง 2 ตัว ตัวเลข 2 จำนวนนี้หมายถึงพิกัดพื้นผิวที่เราใช้เพื่อ "สุ่มตัวอย่าง" ระนาบ 2 มิติที่เราฉายภาพทรงกลมเข้าไป ทำให้เราสามารถกู้คืนเวกเตอร์ต้นฉบับได้ หมายเลขทั้งสองนี้จะสามารถจัดเก็บไว้ใน SNORM8 ได้

รูป 2: การแสดงภาพการทำแผนที่ทรงแปดเหลี่ยม (แหล่งที่มา)

const int BITS = 8

// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
  float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
  vec2 res;
  if (n.z < 0.0) {
    res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
    res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
  } else {
    res.x = n.x * invL1Norm;
    res.y = n.y * invL1Norm;
  }
  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

การลดการบีบอัดในตัวสร้างแสงเงา (Vertex Shape) (เพื่อแปลงกลับไปเป็นพิกัดคาร์ทีเซียน) มีต้นทุนไม่แพง เราไม่เห็นถึงประสิทธิภาพที่ลดลงอย่างมากเมื่อนำเทคนิคนี้ไปใช้ในอุปกรณ์เคลื่อนที่รุ่นใหม่ส่วนใหญ่ การคลายการบีบอัดในตัวปรับแสงเงา Vertex

//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
  vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
  float t = max(-v.z, 0.0);
  v.xy += t * -sign(v.xy);
  return v;

แนวทางนี้ยังใช้เพื่อจัดเก็บพื้นที่แทนเจนต์ทั้งหมดได้ด้วย โดยใช้เทคนิคนี้เพื่อจัดเก็บเวกเตอร์ปกติและเวกเตอร์แทนเจนต์โดยใช้ vec2<SNORM8> แต่คุณต้องหาวิธีจัดเก็บทิศทางของบิตเจนต์ (สำหรับใช้ในสถานการณ์ทั่วไปที่คุณสร้างพิกัดรังสียูวีบนโมเดล) วิธีหนึ่งในการปรับค่านี้คือ จับคู่ส่วนประกอบของการเข้ารหัสเวกเตอร์แทนเจนต์ให้เป็นค่าบวกเสมอ แล้วพลิกเครื่องหมายของกราฟหากคุณต้องการพลิกทิศทางบิตเจนต์และตรวจหาค่าดังกล่าวในเบราว์เซอร์เวอร์เท็กซ์

const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)

// Compressing
for each normal n in mesh:
  //encode to octahedron, result in range [-1, 1]
  vec2 res = vec_to_oct(n);

  // map y to always be positive
  res.y = res.y * 0.5 + 0.5;

  // add a bias so that y is never 0 (sign in the vertex shader)
  if (res.y < bias)
    res.y = bias;

  // Apply the sign of the binormal to y, which was computed elsewhere
  if (binormal_sign < 0)
    res.y *= -1;

  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);

	รูปแบบ	ขนาด
ก่อน	vec3<float32>	12 ไบต์
หลัง	vec2<SNORM8>	2 ไบต์

พิกัดรังสียูวี Vertex

พิกัด UV ซึ่งใช้สำหรับการทำแผนที่พื้นผิว (และสิ่งอื่นๆ) มักจะจัดเก็บโดยใช้จุดลอยตัว 32 บิต การบีบอัดด้วยลอย 16 บิตทำให้เกิดปัญหาด้านความแม่นยำสำหรับพื้นผิวที่มีขนาดใหญ่กว่า 1024x1024 ความแม่นยำของจุดลอยตัวระหว่าง [0.5, 1.0] หมายความว่าค่าจะเพิ่มขึ้นได้มากกว่า 1 พิกเซล

วิธีที่ดีกว่าคือการใช้จำนวนเต็มมาตรฐานที่ไม่มีเครื่องหมาย (UNORM) โดยเฉพาะ UNORM16 วิธีนี้ทำให้มีการกระจายที่สม่ำเสมอทั่วทั้งช่วงพิกัดพื้นผิว รองรับพื้นผิวได้ถึง 65536x65536! โดยสมมติว่าพิกัดพื้นผิวอยู่ในช่วง [0.0, 1.0] ต่อองค์ประกอบ ซึ่งอาจไม่ใช่กรณี ทั้งนี้ขึ้นอยู่กับตาข่าย (ตัวอย่างเช่น ผนังสามารถใช้พิกัดพื้นผิวห่อหุ้มที่มากกว่า 1.0) ดังนั้นโปรดคำนึงถึงเรื่องนี้ด้วยเมื่อดูเทคนิคนี้ ฟังก์ชัน Conversion จะมีลักษณะดังนี้

const int BITS = 16

for each vertex_uv V in mesh:
  V *= clamp(2^BITS - 1, 0, 2^BITS - 1);  // float to integer value conversion

	รูปแบบ	ขนาด
ก่อน	vec2<float32>	8 ไบต์
หลัง	vec2<UNORM16>	4 ไบต์

ผลการบีบอัด Vertex

เทคนิคการบีบอัด Vertex เหล่านี้ทำให้พื้นที่จัดเก็บหน่วยความจำของเวอร์เท็กซ์ลดลง 66% จาก 48 ไบต์ลงเป็น 16 ไบต์ สิ่งนี้ปรากฏว่า:

• แบนด์วิดท์การอ่านหน่วยความจำ Vertex:
  • Binning: 27GB/s ถึง 9GB/s
  • การแสดงผล: 4.5B/วินาที ถึง 1.5 GB/วินาที
• แผง Vertex Fetch:
  • ถังขยะ: 50% ถึง 0%
  • การแสดงผล: 90% ถึง 90%
• ไบต์/เวอร์เท็กซ์เฉลี่ย:
  • Binning: 48B ถึง 16B
  • การแสดงผล: 52B ถึง 18B

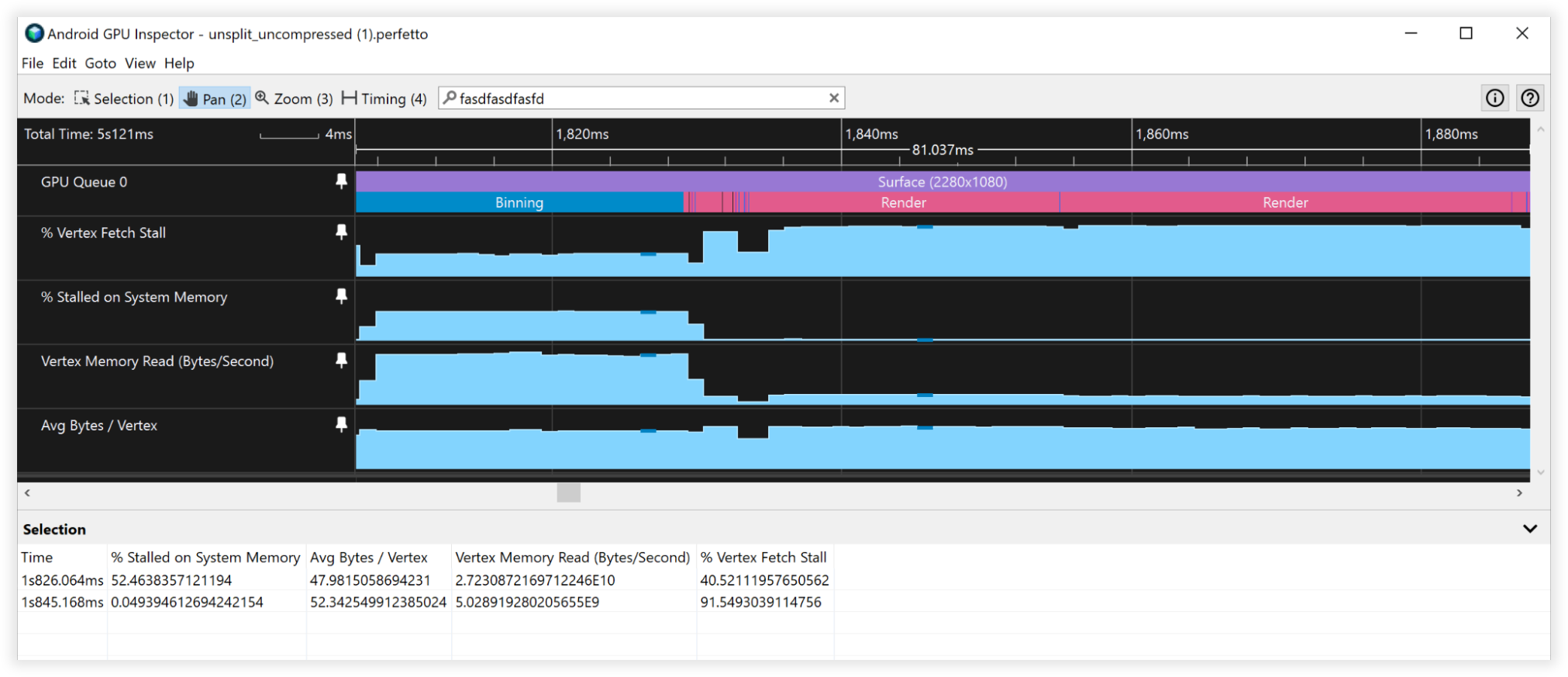
รูป 3: มุมมองเครื่องมือตรวจสอบ GPU ของ Android ของจุดยอดที่ไม่ได้บีบอัด

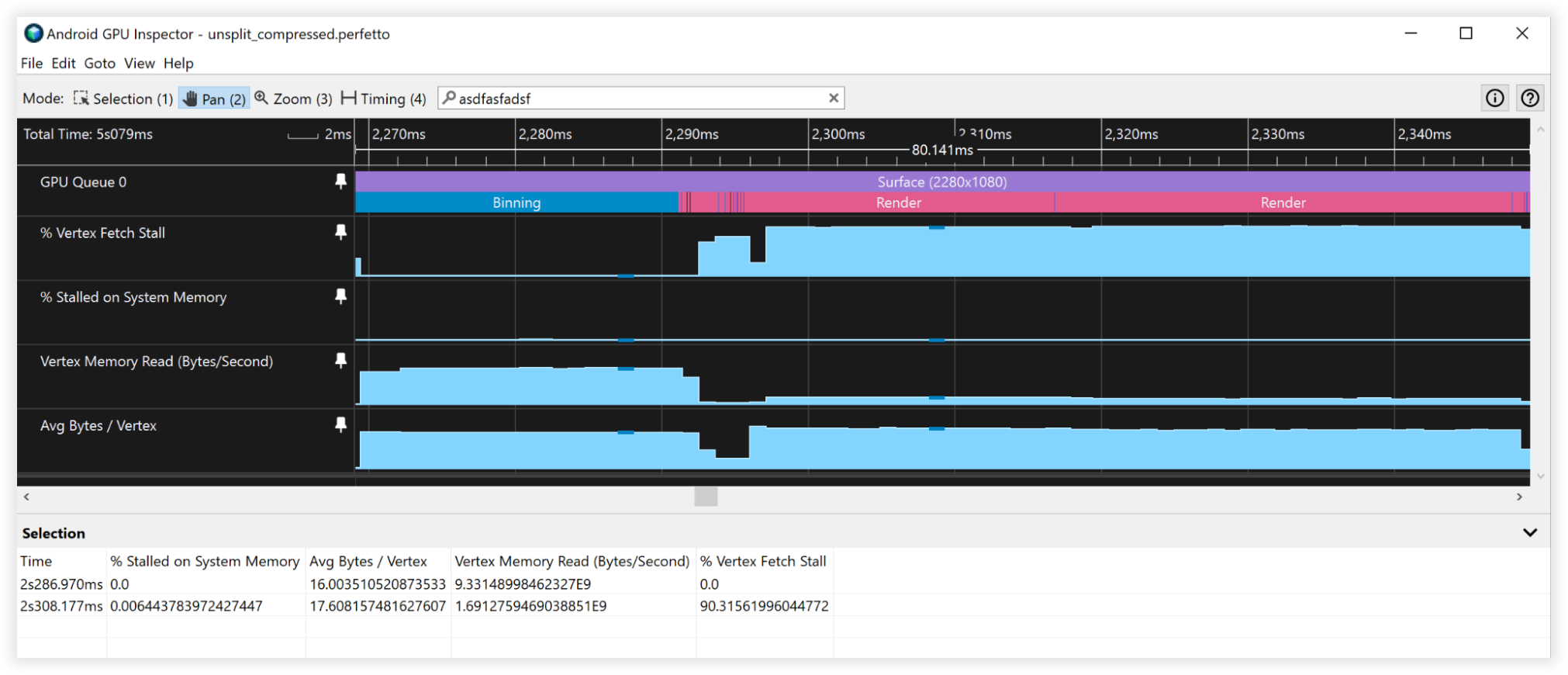
รูป 4: มุมมองเครื่องมือตรวจสอบ GPU Android ของจุดยอดที่บีบอัด

การแยกสตรีม Vertex

Vertex Stream Splitting เพิ่มประสิทธิภาพการจัดระเบียบข้อมูลในบัฟเฟอร์ Vertex นี่เป็นการเพิ่มประสิทธิภาพการทำงานของแคชที่สร้างความแตกต่างใน GPU ตามไทล์ที่มักพบในอุปกรณ์ Android โดยเฉพาะอย่างยิ่งในระหว่างขั้นตอนการเชื่อมโยงของกระบวนการแสดงผล

GPU แบบใช้ไทล์จะสร้างตัวสร้างเฉดสีที่คำนวณพิกัดอุปกรณ์ให้เป็นมาตรฐานโดยอิงตามโหมด Vertex ที่จัดให้มีการทำ Bining ระบบจะดำเนินการกับจุดยอดมุมทุกจุดในฉากก่อน ไม่ว่าจะมองเห็นได้หรือไม่ก็ตาม การเก็บรักษาข้อมูลตำแหน่งจุดยอดมุมได้ต่อเนื่องกันในหน่วยความจำจึงเป็นข้อดีอย่างยิ่ง ส่วนอื่นๆ ที่เลย์เอาต์สตรีม Vertex นี้ใช้ได้ดีคือภาพผ่านเงา เนื่องจากปกติแล้วคุณต้องการเพียงข้อมูลตำแหน่งสำหรับการคำนวณแสงเงา ตลอดจนการข้ามล่วงหน้าของความลึก ซึ่งเป็นเทคนิคที่มักใช้ในการแสดงภาพในคอนโซล/เดสก์ท็อป การจัดวางสตรีม Vertex นี้เหมาะสำหรับเครื่องมือเรนเดอร์หลายคลาส

การแยกสตรีมเกี่ยวข้องกับการตั้งค่าบัฟเฟอร์ Vertex ที่มีส่วนที่ต่อเนื่องกันของข้อมูลตำแหน่งจุดยอดมุม และอีกส่วนหนึ่งที่มีแอตทริบิวต์ Vertex ที่มีการแทรกสลับ แอปพลิเคชันส่วนใหญ่มักจะตั้งค่าบัฟเฟอร์ให้สอดประสานแอตทริบิวต์ทั้งหมดได้อย่างสมบูรณ์ ภาพนี้จะอธิบายความแตกต่าง

Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|

After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|

การดูว่า GPU ดึงข้อมูล Vertex อย่างไรช่วยให้เราเข้าใจข้อดีของ การแยกสตรีม สมมติว่าต้องการอาร์กิวเมนต์:

• บรรทัดแคช 32 ไบต์ (ขนาดค่อนข้างทั่วไป)
• รูปแบบ Vertex ที่ประกอบด้วย
  • ตำแหน่ง, vec3<Flo32> = 12 ไบต์
  • vec3 ปกติ<Flo32> = 12 ไบต์
  • พิกัดรังสียูวี vec2<Flo32> = 8 ไบต์
  • ขนาดโดยรวม = 32 ไบต์

เมื่อ GPU ดึงข้อมูลจากหน่วยความจำเพื่อเชื่อมโยง GPU จะดึงบรรทัดแคชขนาด 32 ไบต์เพื่อดำเนินการ หากไม่มีการแยกสตรีม Vertex จะใช้เพียง 12 ไบต์แรกของบรรทัดแคชนี้สำหรับการเชื่อมโยง และทิ้งอีก 20 ไบต์ที่เหลือเมื่อดึงข้อมูลจุดยอดมุมถัดไป เมื่อใช้การแยกสตรีม Vertex ตำแหน่ง Vertex จะต่อเนื่องกันในหน่วยความจำ ดังนั้นเมื่อมีการดึงข้อมูลชิ้นส่วนขนาด 32 ไบต์เข้าไปในแคช ตำแหน่งดังกล่าวจะมีตำแหน่ง Vertex ทั้งหมด 2 ตำแหน่งสำหรับทำงานก่อนที่จะต้องกลับไปที่หน่วยความจำหลักเพื่อดึงข้อมูลเพิ่ม ซึ่งนับเป็นการปรับปรุง 2 เท่า!

คราวนี้ถ้ารวมการแยกสตรีม Vertex เข้ากับการบีบอัด Vertex เราจะลดขนาดของตำแหน่ง Vertex เดียวลงเหลือ 6 ไบต์ ดังนั้นบรรทัดแคช 32 ไบต์เดี่ยวที่ดึงจากหน่วยความจำของระบบจะมีตำแหน่งเวอร์เท็กซ์ทั้งหมด 5 ตำแหน่งสำหรับทำงาน ซึ่งทำให้การปรับปรุง 5 เท่า!

ผลการแยกสตรีม Vertex

• แบนด์วิดท์การอ่านหน่วยความจำ Vertex:
  • Binning: 27GB/s ถึง 6.5GB/s
  • กำลังแสดงผล: 4.5 GB/วินาที ถึง 4.5 GB/วินาที
• แผง Vertex Fetch:
  • ถังขยะ: 40% ถึง 0%
  • การแสดงผล: 90% ถึง 90%
• ไบต์/เวอร์เท็กซ์เฉลี่ย:
  • Binning: 48B ถึง 12B
  • การแสดงผล: 52B ถึง 52B

รูป 5: มุมมองเครื่องมือตรวจสอบ GPU ของ Android ของสตรีมจุดยอดมุมที่ไม่มีการแยก

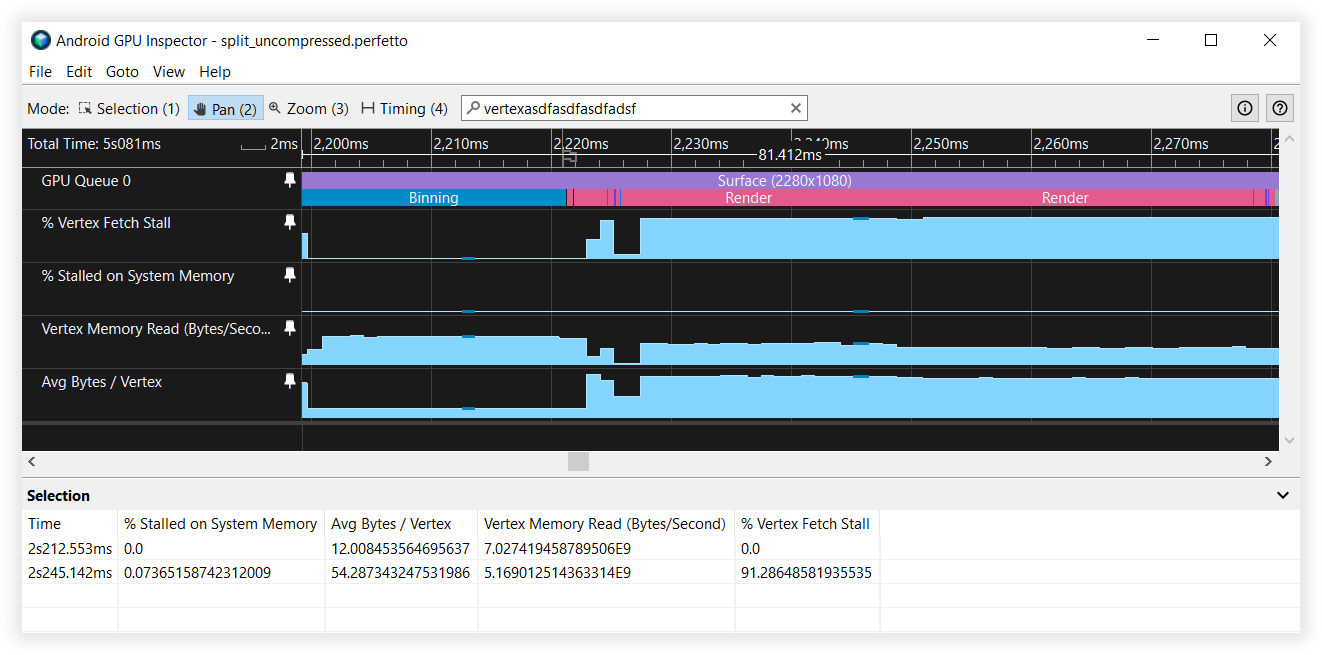
รูป 6: มุมมองเครื่องมือตรวจสอบ GPU ของ Android ของสตรีมจุดยอดมุมแบบแยก

ผลลัพธ์แบบผสม

• แบนด์วิดท์การอ่านหน่วยความจำ Vertex:
  • Binning: 25GB/s ถึง 4.5GB/s
  • กำลังแสดงผล: 4.5 GB/วินาที ถึง 1.7 GB/วินาที
• แผง Vertex Fetch:
  • ถังขยะ: 41% ถึง 0%
  • การแสดงผล: 90% ถึง 90%
• ไบต์/เวอร์เท็กซ์เฉลี่ย:
  • กล่องเก็บ: 48B ถึง 8B
  • การแสดงผล: 52B ถึง 19B

รูป 7: มุมมองเครื่องมือตรวจสอบ GPU ของ Android ของสตรีม Vertex ที่ไม่มีการบีบอัดและไม่มีการบีบอัด

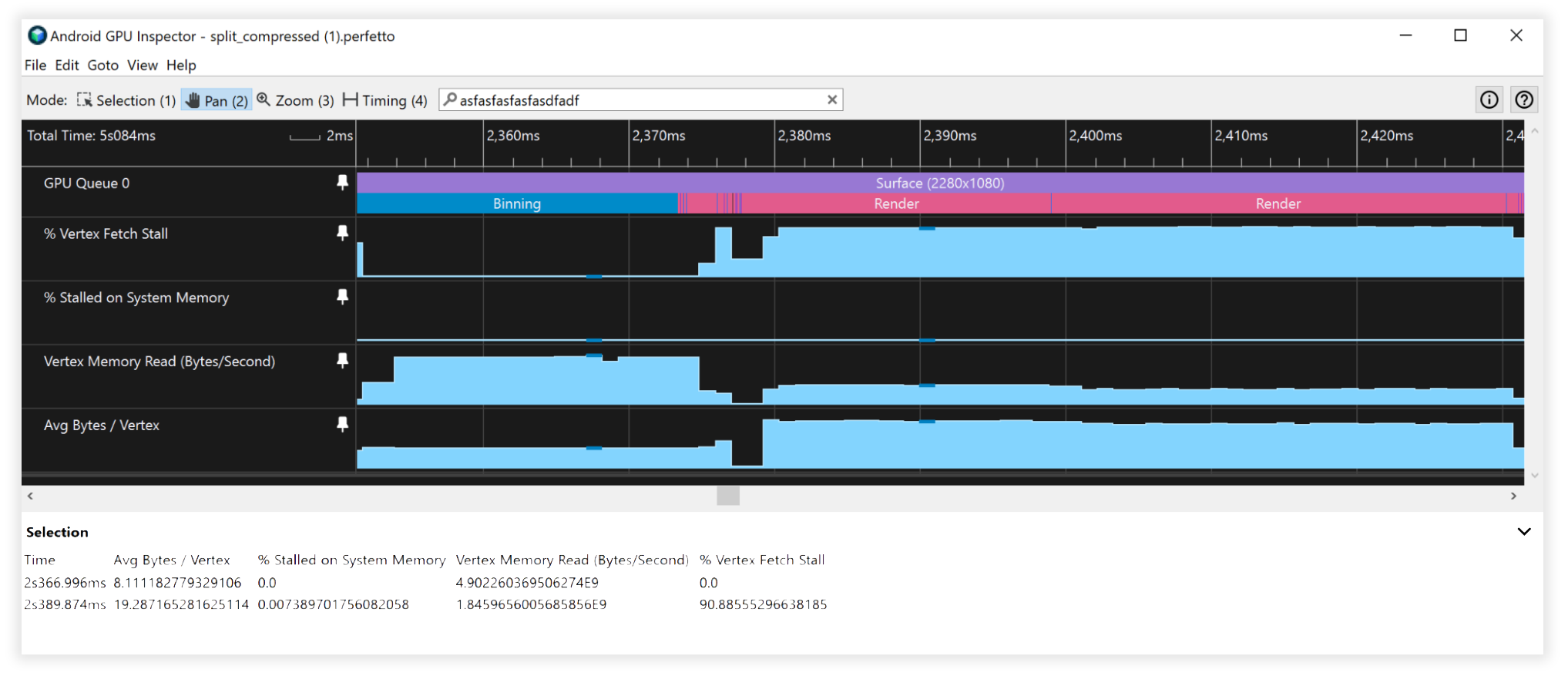
รูป 8: มุมมองเครื่องมือตรวจสอบ GPU ของ Android ของสตรีม Vertex ที่บีบอัดและแยก

ปัจจัยพิจารณาเพิ่มเติม

ข้อมูลบัฟเฟอร์ดัชนี 16 บิตเทียบกับ 32 บิต

• แบ่ง/กลุ่ม Mesh เสมอเพื่อให้พอดีกับบัฟเฟอร์ดัชนี 16 บิต (จุดยอดมุมที่ไม่ซ้ำกันสูงสุด 65,536 จุด) วิธีนี้จะช่วยในการแสดงผลที่จัดทำดัชนีในอุปกรณ์เคลื่อนที่ เนื่องจากการดึงข้อมูลจุดยอดมุมมีราคาถูกกว่าและใช้พลังงานน้อยลง

รูปแบบแอตทริบิวต์บัฟเฟอร์ Vertex ที่ไม่รองรับ

• รูปแบบจุดยอดมุมที่ฉับพลันไม่ได้รับการสนับสนุนอย่างกว้างขวางในอุปกรณ์เคลื่อนที่ และเมื่อใช้แล้วอาจส่งผลเสียต่อประสิทธิภาพซึ่งมีค่าใช้จ่ายสูงในไดรเวอร์ที่พยายามจำลองรูปแบบเหล่านี้หากไม่มีการรองรับฮาร์ดแวร์ ใช้ SNORM เสมอและจ่ายค่า ALU ที่ไม่สำคัญเลยในการขยาย