ניהול נתונים ב-Vertex

פריסת נתונים טובה ודחיסת נתונים הן חלק בלתי נפרד מהביצועים של כל אפליקציה גרפית, בין אם האפליקציה מורכבת מממשקי משתמש בדו-ממד או ממשחק תלת-ממדי גדול בעולם פתוח. בדיקות פנימיות באמצעות Frame Profiler של Android GPU Inspector בעשרות משחקים מובילים ב-Android מצביעות על כך שיש פעולות רבות לשיפור הניהול של נתוני הקודקודים. שמנו לב שמקובל להשתמש בנתוני קודקודים ברמת דיוק מלא, בערכים צפים של 32 ביט לכל מאפייני הקודקודים ובפריסת מאגר נתונים זמני של קודקודים שמשתמשת במערך של מבנים בפורמט עם מאפיינים משולבים לחלוטין.

מאמר זה מסביר איך לבצע אופטימיזציה של הביצועים הגרפיים של אפליקציה ל-Android באמצעות הטכניקות הבאות:

• דחיסת Vertex
• פיצול מקורות נתונים של Vertex

יישום הטכניקות האלה יכול לשפר את השימוש ברוחב פס של קודקודים בשיעור של עד 50%, להפחית את התחרות על ניצול לרעה של הזיכרון עם המעבד (CPU), לצמצם את העומס על זיכרון המערכת ולשפר את חיי הסוללה. ולכולם יש תוצאות טובות גם למפתחים וגם למשתמשי הקצה!

כל הנתונים המוצגים מגיעים מסצנה סטטית לדוגמה שמכילה כ-19,000,000 קודקודים שרצים ב-Pixel 4:

דמות 1: סצנה לדוגמה עם 6 טבעות וקודקודים באורך 19 מ'

דחיסה של Vertex

דחיסה של Vertex הוא מונח כולל לשיטות דחיסה עם איבוד נתונים להשתמש באריזה יעילה כדי להקטין את הגודל של נתוני הקודקודים גם בזמן הריצה וגם באחסון. להקטנת גודל הקודקודים יש כמה יתרונות, כולל צמצום רוחב הפס של הזיכרון ב-GPU (על ידי סחר במחשוב ברוחב פס), שיפור השימוש במטמון וצמצום הסיכון לרישומי דליפה.

הגישות הנפוצות לדחיסת Vertex כוללות:

• הקטנת הדיוק המספרי של מאפייני נתוני קודקוד (לדוגמה: מספר ממשי (float) של 32 ביט ל-float של 16 ביט)
• ייצוג המאפיינים בפורמטים שונים

לדוגמה, אם קודקוד משתמש בצפים מלאים של 32 ביט למיקום (vec3), נורמלי (vec3) וקואורדינטה מרקם (vec2), החלפת כל אלה בצפים של 16 ביט תקטין את גודל הקודקוד ב-50% (16 בייט בקודקוד ממוצע של 32 בייטים).

מיקומים של קודקוד

ניתן לדחוס נתוני מיקום של Vertex מערכי נקודה צפה בדיוק של 32 ביט לערכים של נקודה צפה בחצי דיוק של 16 ביט ברוב המכריע. ברוב המכשירים הניידים יש תמיכה בחצי צפים. פונקציית המרה שעוברת מ-float32 ל-float16 נראית כך (הותאמה מהמדריך הזה):

uint16_t f32_to_f16(float f) {
  uint32_t x = (uint32_t)f;
  uint32_t sign = (unsigned short)(x >> 31);
  uint32_t mantissa;
  uint32_t exp;
  uint16_t hf;

  mantissa = x & ((1 << 23) - 1);
  exp = x & (0xFF << 23);
  if (exp >= 0x47800000) {
    // check if the original number is a NaN
    if (mantissa && (exp == (0xFF << 23))) {
      // single precision NaN
      mantissa = (1 << 23) - 1;
    } else {
      // half-float will be Inf
      mantissa = 0;
    }
    hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
         (uint16_t)(mantissa >> 13);
  }
  // check if exponent is <= -15
  else if (exp <= 0x38000000) {
    hf = 0;  // too small to be represented
  } else {
    hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
         (uint16_t)(mantissa >> 13);
  }

  return hf;
}

יש הגבלה לגישה הזו; רמת הדיוק פוחתת ככל שהקודד רחוק יותר מהמקור, ולכן הוא פחות מתאים לרשתות עם נפח גדול מאוד מבחינה מרחבית (קודקודים שמכילים יסודות מעבר ל-1024). ניתן לטפל בכך על ידי פיצול רשת למקטעי נתונים קטנים יותר, מרכז כל מקטעים סביב מקור המודל ושינוי קנה המידה כך שכל הקודקודים של כל מקטע יתאים לטווח [-1, 1], שמכיל את הדיוק הגבוה ביותר עבור ערכי נקודות צפות. הקוד המדומה לדחיסה נראה כך:

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));

אופים את הגורם לקביעת קנה המידה ואת התרגום למטריצת המודל כדי לפרוס את נתוני הקודקודים במהלך העיבוד. חשוב לזכור שאתם לא רוצים להשתמש באותה מטריצת המודל לשינוי נורמליות, כי לא הופעלה בהם אותה דחיסה. תצטרכו מטריצה ללא הטרנספורמציות לביטול הדחיסה האלה עבור נורמלים, או להשתמש במטריצת המודל הבסיסית (שבה ניתן להשתמש לנורמלים) ולאחר מכן להחיל את הטרנספורמציות הנוספות לביטול הדחיסה על מטריצת המודל שבתוך כלי ההצללה. לדוגמה:

vec3 in in_pos;

void main() {
   ...
   // bounding box data packed into uniform buffer
   vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
   gl_Position = proj * view * model * decompress_pos;
}

גישה אחרת כוללת שימוש במספרים מנורמלים חתומים (SNORM). סוגי הנתונים SNORM משתמשים במספרים שלמים ולא בנקודה צפה כדי לייצג ערכים בין [ -1, 1]. שימוש ב-SNORM של 16 סיביות למיקומים מאפשר לך ליהנות מאותם חיסכון בזיכרון של float16, ללא החסרונות של התפלגויות לא אחידות. הטמעה מומלצת לשימוש ב-SNORM נראית כך:

const int BITS = 16

for each position p in Mesh:
   p -= center_of_bounding_box // Moves Mesh back to the center of model space
   p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
   // float to integer value conversion
   p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1) 

	פורמט	גודל
לפני	vec4<float32>	16 בייטים
אחרי	vec3<float16/SNORM16>	6 בייטים

נורמליות ומרחב משיק של Vertex

נורמליות של Vertex דרושים לתאורה, ושטח הטנגנס נדרש לטכניקות מורכבות יותר, כמו מיפוי רגיל.

מרחב משיק

מרחב הטנגנס הוא מערכת קואורדינטות שבה כל קודקוד מורכב מווקטור רגיל, טנגנס ביטנגנס. מכיוון ששלושת הווקטורים האלה בדרך כלל אורתוגונליים זה לזה, אנחנו צריכים לאחסן רק שניים מהם ויכולים לחשב את השלישי על ידי שימוש במכפלה מוצלבת של שני הווקטורים האחרים בצללית הקודקוד.

בדרך כלל ניתן לייצג את הווקטורים האלה באמצעות צפים של 16 ביט ללא פגיעה תפיסתית במהימנות החזותית, אז זה מקום טוב להתחיל בו!

אפשר להמשיך לדחוס את הנתונים בעזרת שיטה שנקראת QTangents, שמאחסנת את כל מרחב המשיק בקוואטרניון אחד. מכיוון שניתן להשתמש בקווטרניונים כדי לייצג סיבובים, על ידי מחשבה על וקטורי המרחב של הטנגנס בתור וקטורים של עמודות של מטריצה בגודל 3x3, שמייצגים סיבוב (במקרה הזה, ממרחב המודל למרחב המשיק), אפשר להמיר בין השניים! אפשר להתייחס לקווטרניון ברמת הנתונים של vec4, ולהמיר

const int BITS = 16

quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
   mat3 tbn = {normal, tangent, bitangent};
   quaternion qTangent(tbn);
   qTangent.normalize();

   //Make sure QTangent is always positive
   if (qTangent.w < 0)
       qTangent = -qTangent;

   const float bias = 1.0 / (2^(BITS - 1) - 1);

   //Because '-0' sign information is lost when using integers,
   //we need to apply a "bias"; while making sure the Quaternion
   //stays normalized.
   // ** Also our shaders assume qTangent.w is never 0. **
   if (qTangent.w < bias) {
       Real normFactor = Math::Sqrt( 1 - bias * bias );
       qTangent.w = bias;
       qTangent.x *= normFactor;
       qTangent.y *= normFactor;
       qTangent.z *= normFactor;
   }

   //If it's reflected, then make sure .w is negative.
   vec3 naturalBinormal = cross_product(tangent, normal);
   if (dot_product(naturalBinormal, binormal) <= 0)
       qTangent = -qTangent;
   return qTangent;
}

הקווטרניון יעבור נירמול ותוכלו לדחוס אותו באמצעות SNORMs. רכיבי SNORM של 16 סיביות מעניקים רמת דיוק טובה וחיסכון בזיכרון. מעבדי SNORM עם 8 ביט יכולים לחסוך עוד יותר, אבל הם עלולים לגרום לשיבושים בחומרים ספקולטיביים מאוד. אפשר לנסות את שניהם ולבדוק מה הכי מתאים לנכסים שלך. קידוד הקווטרניון נראה כך:

for each vertex v in mesh:
   quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
   // Once we have the quaternion we can compress it
   res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);

כדי לפענח את הקווטרנטיון בתוכנת ההצללה של הקודקוד (הותאם מכאן):

vec3 xAxis( vec4 qQuat )
{
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwy = fTy * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxy = fTy * qQuat.x;
  float fTxz = fTz * qQuat.x;
  float fTyy = fTy * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}

vec3 yAxis( vec4 qQuat )
{
  float fTx  = 2.0 * qQuat.x;
  float fTy  = 2.0 * qQuat.y;
  float fTz  = 2.0 * qQuat.z;
  float fTwx = fTx * qQuat.w;
  float fTwz = fTz * qQuat.w;
  float fTxx = fTx * qQuat.x;
  float fTxy = fTy * qQuat.x;
  float fTyz = fTz * qQuat.y;
  float fTzz = fTz * qQuat.z;

  return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}

void main() {
  vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
  vec3 normal = xAxis(qtangent);
  vec3 tangent = yAxis(qtangent);
  float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
  vec3 binormal = cross(normal, tangent) * biNormalReflection;
  ...
}

	פורמט	גודל
לפני	vec3<float32> + vec3<float32> + vec3<float32>	36 בייטים
אחרי	vec4<SNORM16>	8 בייטים

רגילים בלבד

אם אתם צריכים רק לאחסן וקטורים נורמליים, יש גישה אחרת שיכולה לחסוך יותר – שימוש במיפוי אוקטהדראלי של וקטורים של יחידות במקום בקואורדינטות קרטזיות כדי לדחוס את הווקטור הנורמלי. מיפוי אוקטהדרלי פועל על ידי הקרנת כדור יחידה לאקטהדרון, ואז הטייה של האוקטהדרון למישור דו-ממדי. התוצאה היא שאפשר לייצג כל וקטור נורמלי באמצעות שני מספרים בלבד. ניתן להתייחס לשני המספרים האלה כקואורדינטות של טקסטורה שבהן אנחנו משתמשים כדי "לדגום" את המישור הדו-ממדי שעליו הקרנתם את הכדור, וכך לאפשר לנו לשחזר את הווקטור המקורי. לאחר מכן אפשר לאחסן את שני המספרים האלה ב-SNORM8.

דמות 2:מיפוי אוקטהדרלי באופן חזותי (מקור)

const int BITS = 8

// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
  float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
  vec2 res;
  if (n.z < 0.0) {
    res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
    res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
  } else {
    res.x = n.x * invL1Norm;
    res.y = n.y * invL1Norm;
  }
  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

ביטול הדחיסה בתוכנת ההצללה (shader) של קודקוד (כדי להמיר בחזרה לקואורדינטות קרטזיות) הוא לא יקר; ברוב המכשירים הניידים המודרניים, לא ראינו ירידה משמעותית בביצועים במהלך יישום השיטה הזו. ביטול הדחיסה בתוכנת ההצללה של קודקוד:

//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
  vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
  float t = max(-v.z, 0.0);
  v.xy += t * -sign(v.xy);
  return v;

אפשר להשתמש בגישה הזו גם כדי לאחסן את כל שטח המשיק ולאחסן את הווקטור הנורמלי והטנגנס באמצעות vec2<SNORM8> אבל עליכם למצוא דרך לאחסן את הכיוון של הביטנגנס (נדרש לתרחיש נפוץ שבו שיקוף הקואורדינטות של קרינת UV בדגם מסוים). דרך אחת ליישם זאת היא למפות רכיב בקידוד הווקטור של הטנגנס כך שיהיה תמיד חיובי, ואז להפוך את הסימן שלו אם צריכים להפוך את הכיוון של הביטנגנס ולבדוק אותו בהצללה של הקודקוד:

const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)

// Compressing
for each normal n in mesh:
  //encode to octahedron, result in range [-1, 1]
  vec2 res = vec_to_oct(n);

  // map y to always be positive
  res.y = res.y * 0.5 + 0.5;

  // add a bias so that y is never 0 (sign in the vertex shader)
  if (res.y < bias)
    res.y = bias;

  // Apply the sign of the binormal to y, which was computed elsewhere
  if (binormal_sign < 0)
    res.y *= -1;

  res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)

// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);

	פורמט	גודל
לפני	vec3<float32>	12 בייטים
אחרי	vec2<SNORM8>	2 בייטים

קואורדינטות UV ב-Vertex

קואורדינטות UV, המשמשות למיפוי טקסטורות (בין היתר), נשמרות בדרך כלל באמצעות ציפה של 32 ביט. דחיסת הנתונים באמצעות צפופים של 16 ביט גורמת לבעיות דיוק במרקמים שגדולים מ-1024x1024. המשמעות של רמת הדיוק של נקודה צפה (floating-point) היא [0.5, 1.0], וכתוצאה מכך הערכים יגדלו בפיקסל אחד!

הגישה הטובה יותר היא להשתמש במספרים שלמים מנורמלים לא חתומים (UNORM), ובמיוחד UNORM16. הדבר מספק התפלגות אחידה בכל טווח הקואורדינטות של המרקם, תוך תמיכה במרקמים בגודל של עד 65536x65536! ההנחה היא שהקואורדינטות של המרקם נמצאות בטווח [0.0, 1.0] לכל אלמנט, וייתכן שלא כך זה יהיה המצב בהתאם לרשת (לדוגמה, קירות יכולים להשתמש בקואורדינטות של טקסטורה גולשות מעבר ל-1.0), ולכן חשוב לזכור זאת כשבוחנים את השיטה הזו. פונקציית ההמרה תיראה כך:

const int BITS = 16

for each vertex_uv V in mesh:
  V *= clamp(2^BITS - 1, 0, 2^BITS - 1);  // float to integer value conversion

	פורמט	גודל
לפני	vec2<float32>	8 בייטים
אחרי	vec2<UNORM16>	4 בייטים

תוצאות דחיסה של Vertex

טכניקות דחיסת הקודקודים הובילו לירידה של 66% בנפח אחסון הזיכרון של קודקודים, מ-48 בייטים ל-16 בייטים. העובדה הזו מתבטאת ב:

• רוחב הפס לקריאת זיכרון Vertex:
  • חיתוך: 27GB/s עד 9GB/s
  • רינדור: 4.5B לשנייה עד 1.5GB לשנייה
• דוכןי אחזור של Vertex:
  • חיתוך: 50% עד 0%
  • רינדור: 90% עד 90%
• בייטים/Vertex ממוצעים:
  • Binning: 48B עד 16B
  • רינדור: 52B עד 18B

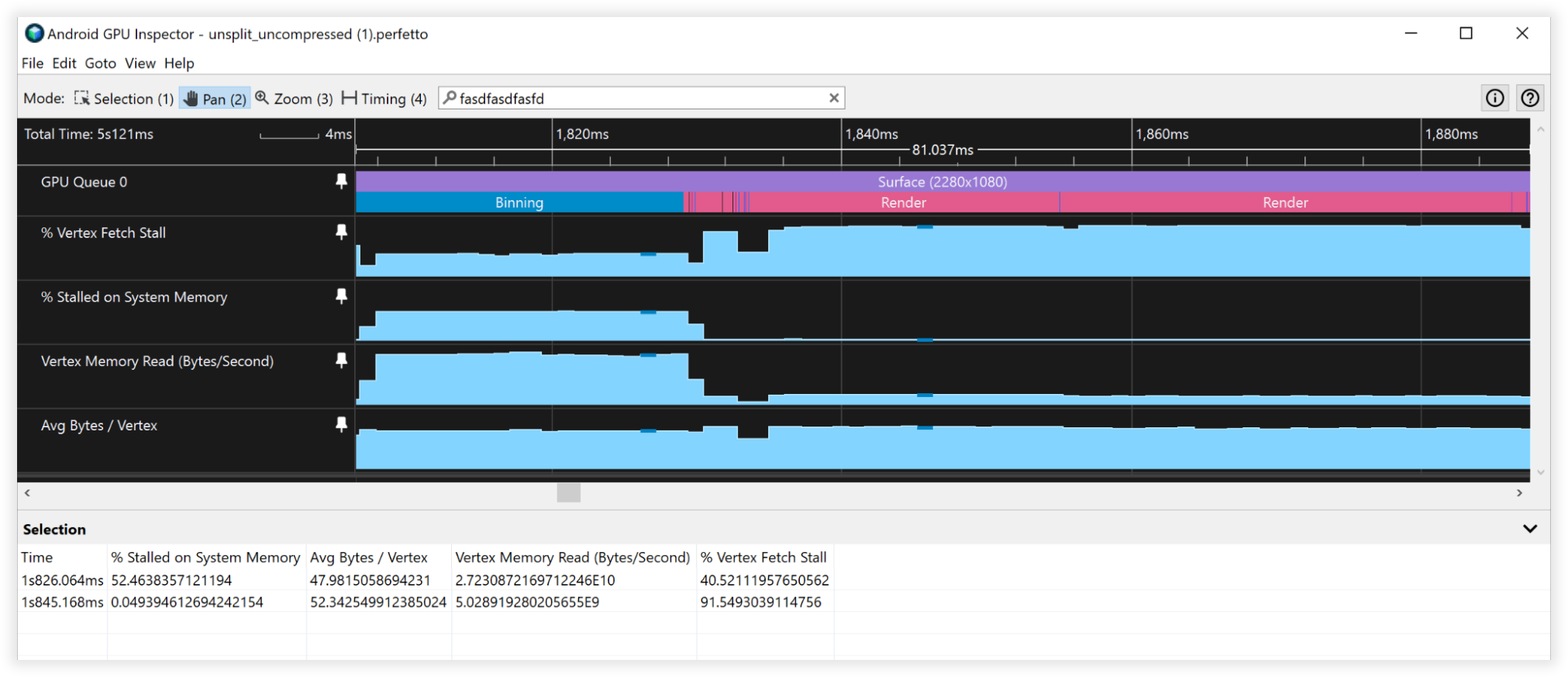
דמות 3: תצוגת Android GPU Inspector של קודקודים לא דחוסים

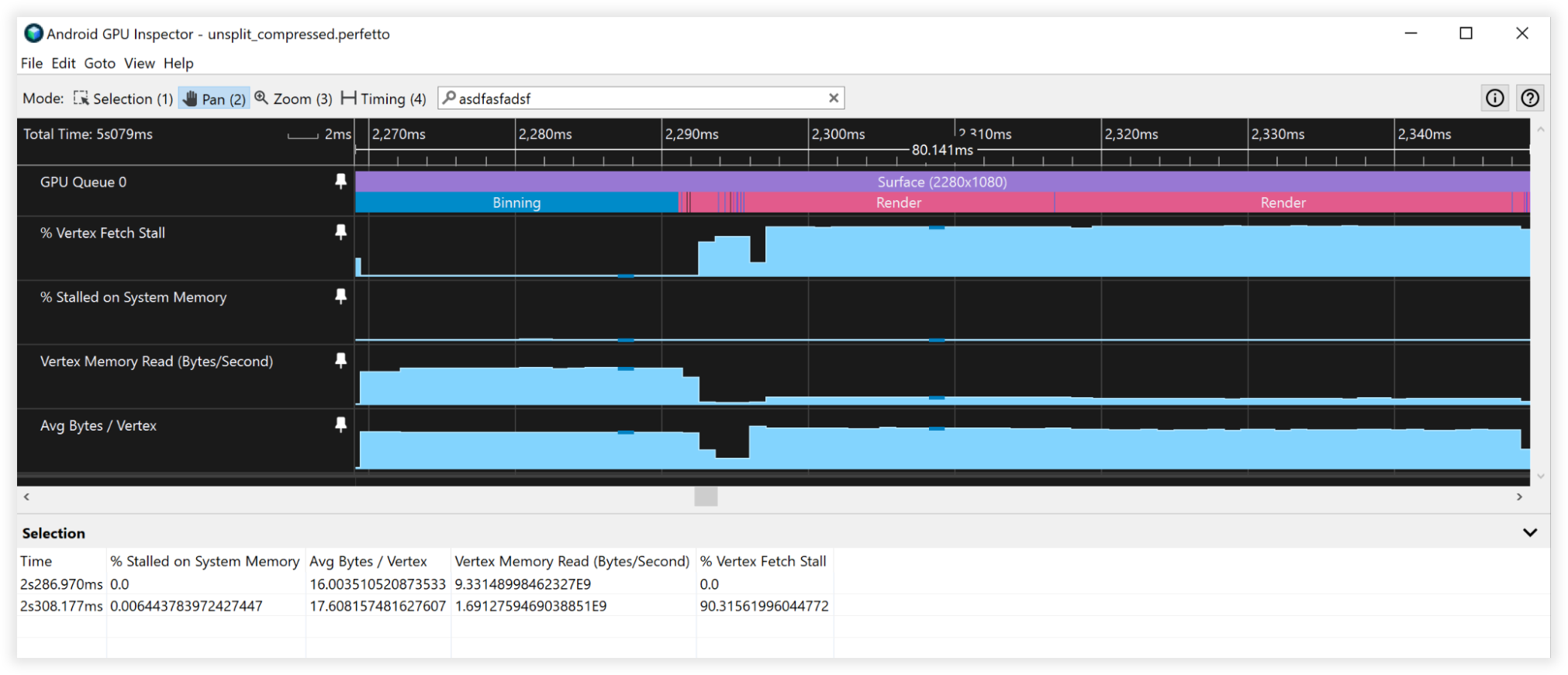
דמות 4: תצוגת Android GPU Inspector של קודקודים דחוסים

פיצול מקורות נתונים של Vertex

Vertex Stream Splitting מבצעת אופטימיזציה של ארגון הנתונים במאגר הנתונים הזמני של הקודקוד. זוהי אופטימיזציה של ביצועי המטמון שגורמת לשינוי במעבדי GPU מבוססי משבצות שבדרך כלל נמצאים במכשירי Android – בפרט בשלב ה-Binger של תהליך העיבוד.

יחידות GPU המבוססות על משבצות יוצרות הצללה שמחשבת את הקואורדינטות של המכשיר המנורמלות על סמך תוכנת ההצללה (shader) שסופקה על ידי קודקוד. הפעולה מבוצעת קודם בכל קודקוד בסצנה, גם אם היא גלויה וגם אם לא. לכן, שמירה על רציפות בזיכרון של נתוני מיקום הקודקוד היא יתרון גדול. מקומות נוספים שבהם הפריסה של זרם הקודקוד יכולה להיות שימושית היא מעברי צלליות. מכיוון שבדרך כלל צריך רק נתוני מיקום לצורך חישובי צלליות, והקדמה לעומק. השיטה הזו משמשת בדרך כלל לעיבוד של קונסולה או מחשב. הפריסה הזו של זרם קודקוד יכולה לנצח עבור מספר מחלקות של מנוע הרינדור!

פיצול סטרימינג כולל הגדרה של מאגר הנתונים הזמני של קודקוד עם קטע רציף של נתוני מיקום הקודקוד וקטע נוסף שמכיל מאפייני קודקודים משולבים. בדרך כלל, רוב האפליקציות מגדירות את מאגרי הנתונים הזמניים באופן מלא שמשלב בין כל המאפיינים. באיור הזה מוסבר את ההבדל:

Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|

After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|

לבחון איך ה-GPU מאחזר נתוני קודקודים, עוזר לנו להבין את היתרונות של של פיצול נתונים בסטרימינג. בהנחה לצורך הוויכוח:

• שורות מטמון של 32 בייטים (גודל די נפוץ)
• פורמט של Vertex שכולל:
  • מיקום, vec3<float32> = 12 בייטים
  • vec3 רגיל<float32> = 12 בייטים
  • קואורדינטות של קרינת UV vec2<float32> = 8 בייטים
  • גודל כולל = 32 בייטים

כשה-GPU מאחזר נתונים מהזיכרון לצורך binning, הוא יאחזר קו מטמון של 32 בייט כדי לעבוד עליו. אם לא יפוצלו את הקוד של זרם הקוד, המערכת תשתמש בפועל רק ב-12 הבייטים הראשונים של שורת המטמון הזו לצורך יצירת מקבצים, ותמחק את 20 הבייטים האחרים כשהוא יאחזר את הקודקוד הבא. במקרה של פיצול זרם קודקוד, מיקומי הקודקודים יהיו רציפים בזיכרון, כך שכאשר מקטע של 32 בייטים יישלף למטמון, הוא יכיל למעשה שני מיקומי קודקודים שלמים שאפשר לעבוד עליהם לפני שיהיה צורך לחזור לזיכרון הראשי כדי לאחזר עוד, שיפור פי 2!

עכשיו, אם נשלב את הפיצול של זרם הקודקוד עם דחיסת קודקוד, נקטין את הגודל של מיקום קודקוד יחיד ל-6 בייטים. כך, שורת מטמון אחת של 32 בייטים שנשלפה מזיכרון המערכת תכלול 5 מיקומי קודקודים שלמים שאפשר לפעול עליהם, שיפור של פי 5!

תוצאות הפיצול של מקורות נתונים מ-Vertex

• רוחב הפס לקריאת זיכרון Vertex:
  • צמצום: 27GB/s עד 6.5GB/s
  • רינדור: 4.5GB/s עד 4.5GB/s
• דוכןי אחזור של Vertex:
  • חיתוך: 40% עד 0%
  • רינדור: 90% עד 90%
• בייטים/Vertex ממוצעים:
  • Binning: 48B עד 12B
  • רינדור: 52B עד 52B

דמות 5: תצוגת Android GPU Inspector של עדכוני קודקוד לא מפוצלים

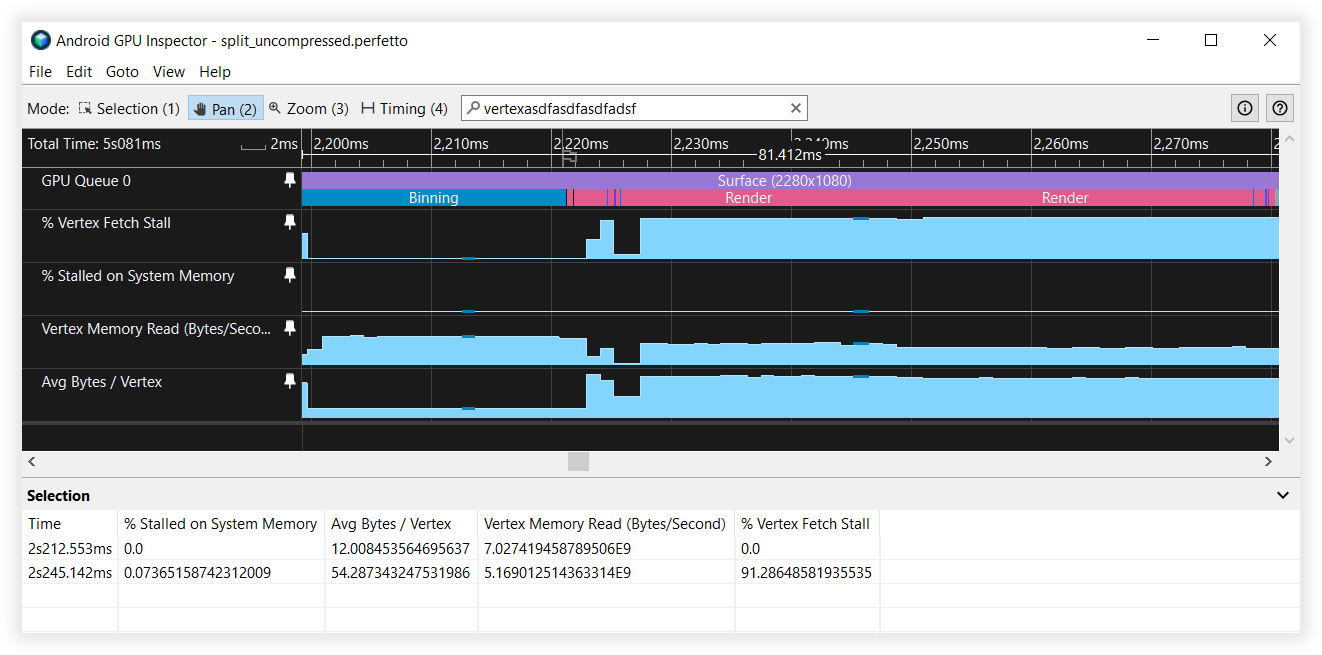
דמות 6: תצוגת Android GPU Inspector של סטרימינג מפוצל של קודקוד

תוצאות מורכבות

• רוחב הפס לקריאת זיכרון Vertex:
  • חיתוך: 25GB/s עד 4.5GB/s
  • רינדור: 4.5GB/s עד 1.7GB/s
• דוכןי אחזור של Vertex:
  • חיתוך: 41% עד 0%
  • רינדור: 90% עד 90%
• בייטים/Vertex ממוצעים:
  • Binning: 48B עד 8B
  • רינדור: 52B עד 19B

דמות 7: תצוגת Android GPU Inspector של שידורי קודקוד לא מפוצלים ולא מפוצלים

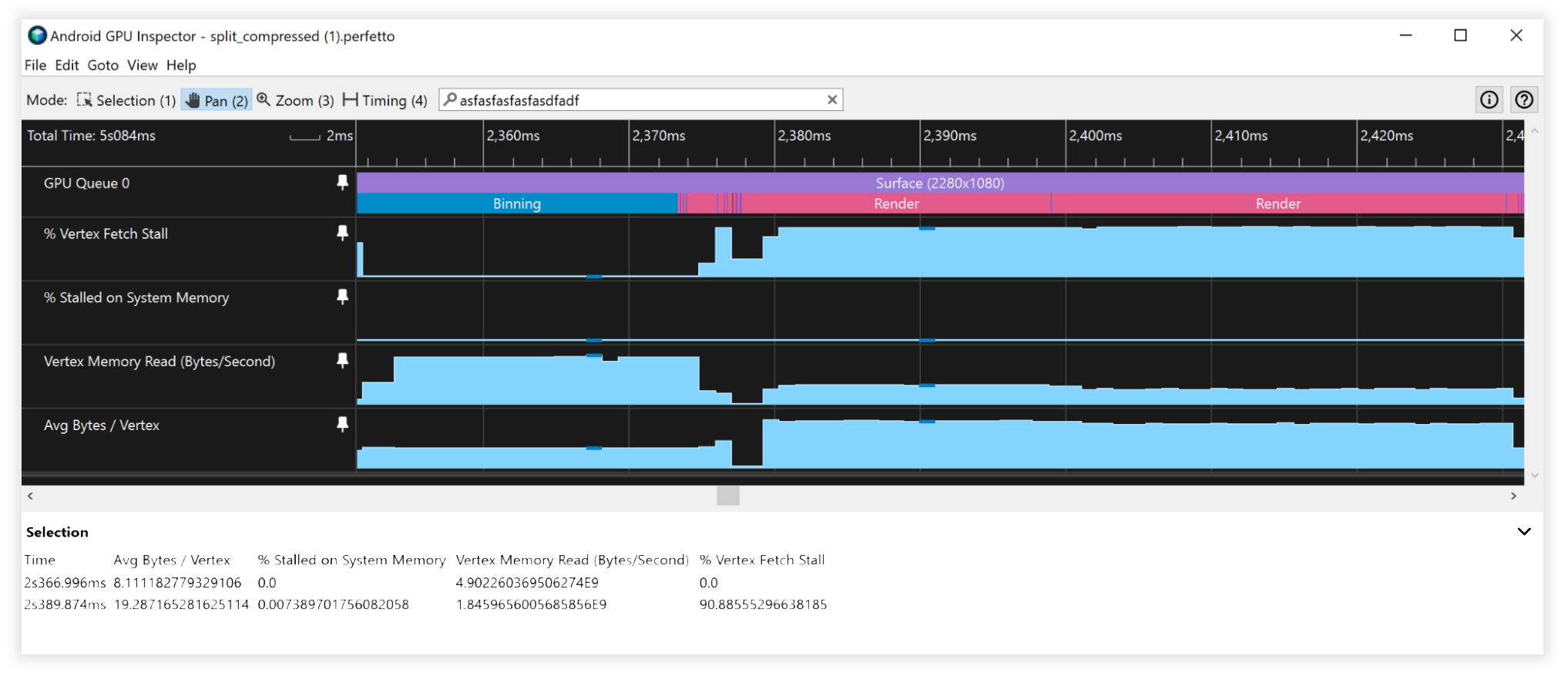
דמות 8: תצוגה של Android GPU Inspector של סטרימינג מפוצל ודחוס של קודקוד

שיקולים נוספים

נתוני מאגר נתונים זמני של אינדקס 16 לעומת 32 ביט

• תמיד חשוב לפצל/מקטעים כדי שיתאימו למאגר הנתונים הזמני של 16 ביט (עד 65,536 קודקודים ייחודיים). כך תוכלו לעבד בנייד את הנתונים שנוספו לאינדקס כי זול יותר לאחזר נתוני קודקודים והם צורכים פחות חשמל.

פורמטים לא נתמכים של מאפייני מאגר נתונים זמני של Vertex

• בניידים אין תמיכה רחבה בפורמטים של קודקוד SSCALED. כשמשתמשים בהם, יכולים להיות ירידות בביצועים אם אין תמיכה בחומרה של נהגים שמנסים לחקות אותם. תמיד צריך לעבור על SNORM ולשלם את עלות ה-ALU הזניחה כדי לבטל את הדחיסה.