ভাল ভার্টেক্স ডেটা লেআউট এবং কম্প্রেশন যেকোন গ্রাফিকাল অ্যাপ্লিকেশনের পারফরম্যান্সের অবিচ্ছেদ্য অংশ, একটি অ্যাপ্লিকেশন 2D ব্যবহারকারী ইন্টারফেস নিয়ে গঠিত বা একটি বড় 3D ওপেন ওয়ার্ল্ড গেম। কয়েক ডজন শীর্ষ Android গেমগুলিতে Android GPU ইন্সপেক্টরের ফ্রেম প্রোফাইলারের সাথে অভ্যন্তরীণ পরীক্ষা ইঙ্গিত দেয় যে ভার্টেক্স ডেটা ব্যবস্থাপনা উন্নত করতে অনেক কিছু করা যেতে পারে। আমরা লক্ষ্য করেছি যে ভার্টেক্স ডেটার জন্য সম্পূর্ণ নির্ভুলতা, সমস্ত ভার্টেক্স অ্যাট্রিবিউটের জন্য 32-বিট ফ্লোট মান এবং একটি ভার্টেক্স বাফার লেআউট যা সম্পূর্ণ ইন্টারলিভড অ্যাট্রিবিউটের সাথে ফর্ম্যাট করা কাঠামোর অ্যারে ব্যবহার করে।
নিম্নলিখিত কৌশলগুলি ব্যবহার করে কীভাবে আপনার অ্যান্ড্রয়েড অ্যাপ্লিকেশনের গ্রাফিক্স কর্মক্ষমতা অপ্টিমাইজ করবেন তা এই নিবন্ধটি আলোচনা করে:
- ভার্টেক্স কম্প্রেশন
- ভার্টেক্স স্ট্রীম স্প্লিটিং
এই কৌশলগুলি প্রয়োগ করা ভার্টেক্স মেমরি ব্যান্ডউইথের ব্যবহারকে 50% পর্যন্ত উন্নত করতে পারে, CPU এর সাথে মেমরি বাসের বিরোধ কমাতে পারে, সিস্টেম মেমরিতে স্টল কমাতে পারে এবং ব্যাটারির আয়ু উন্নত করতে পারে; যার সবই ডেভেলপার এবং শেষ ব্যবহারকারী উভয়ের জন্যই জয়ী!
উপস্থাপিত সমস্ত ডেটা একটি Pixel 4 এ চলমান ~19,000,000 শীর্ষবিন্দু ধারণকারী একটি উদাহরণ স্ট্যাটিক দৃশ্য থেকে আসে:

চিত্র 1: 6টি রিং এবং 19m শীর্ষবিন্দু সহ নমুনা দৃশ্য
ভার্টেক্স কম্প্রেশন
ভার্টেক্স কম্প্রেশন ক্ষতিকারক কম্প্রেশন কৌশলগুলির জন্য একটি ছাতা শব্দ যা রানটাইম এবং স্টোরেজ উভয় সময়ে ভার্টেক্স ডেটার আকার কমাতে দক্ষ প্যাকিং ব্যবহার করে। শীর্ষবিন্দুগুলির আকার হ্রাস করার অনেকগুলি সুবিধা রয়েছে, যার মধ্যে রয়েছে GPU-তে মেমরি ব্যান্ডউইথ হ্রাস করা (ব্যান্ডউইথের জন্য ট্রেডিং কম্পিউটের মাধ্যমে), ক্যাশের ব্যবহার উন্নত করা এবং সম্ভাব্যভাবে রেজিস্টার ছড়িয়ে পড়ার ঝুঁকি হ্রাস করা।
ভার্টেক্স কম্প্রেশনের সাধারণ পদ্ধতির মধ্যে রয়েছে:
- ভার্টেক্স ডেটা অ্যাট্রিবিউটের সংখ্যাগত নির্ভুলতা হ্রাস করা (যেমন: 32-বিট ফ্লোট থেকে 16-বিট ফ্লোট)
- বিভিন্ন বিন্যাসে গুণাবলী প্রতিনিধিত্ব
উদাহরণস্বরূপ, যদি একটি শীর্ষস্থানীয় অবস্থান (vec3), স্বাভাবিক (vec3) এবং টেক্সচার কোঅর্ডিনেট (vec2) এর জন্য সম্পূর্ণ 32-বিট ফ্লোট ব্যবহার করে, তাহলে এই সমস্তগুলিকে 16-বিট ফ্লোট দিয়ে প্রতিস্থাপন করলে শীর্ষবিন্দুর আকার 50% কমে যাবে (16 বাইট অন গড় 32 বাইট শীর্ষবিন্দু)।
শীর্ষস্থানীয় অবস্থান
ভার্টেক্স পজিশন ডেটা সম্পূর্ণ নির্ভুলতা 32-বিট ফ্লোটিং পয়েন্ট মান থেকে অর্ধ নির্ভুল 16-বিট ফ্লোটিং পয়েন্ট মানগুলিতে সংকুচিত করা যেতে পারে এবং বেশিরভাগ মেশে হার্ডওয়্যারে অর্ধেক ফ্লোটগুলি সমর্থিত। float32 থেকে float16 এ যাওয়া একটি রূপান্তর ফাংশন এইরকম দেখায় ( এই নির্দেশিকা থেকে অভিযোজিত ):
uint16_t f32_to_f16(float f) {
uint32_t x = (uint32_t)f;
uint32_t sign = (unsigned short)(x >> 31);
uint32_t mantissa;
uint32_t exp;
uint16_t hf;
mantissa = x & ((1 << 23) - 1);
exp = x & (0xFF << 23);
if (exp >= 0x47800000) {
// check if the original number is a NaN
if (mantissa && (exp == (0xFF << 23))) {
// single precision NaN
mantissa = (1 << 23) - 1;
} else {
// half-float will be Inf
mantissa = 0;
}
hf = (((uint16_t)sign) << 15) | (uint16_t)((0x1F << 10)) |
(uint16_t)(mantissa >> 13);
}
// check if exponent is <= -15
else if (exp <= 0x38000000) {
hf = 0; // too small to be represented
} else {
hf = (((uint16_t)sign) << 15) | (uint16_t)((exp - 0x38000000) >> 13) |
(uint16_t)(mantissa >> 13);
}
return hf;
}
এই পদ্ধতির একটি সীমাবদ্ধতা আছে; সূক্ষ্মতা হ্রাস পায় কারণ শীর্ষবিন্দু উৎপত্তি থেকে দূরে চলে যায়, এটি স্থানিকভাবে খুব বড় জালের জন্য কম উপযোগী করে তোলে (যে শীর্ষস্থানে উপাদান রয়েছে যা 1024 ছাড়িয়ে যায়)। আপনি একটি জালকে ছোট ছোট খণ্ডে বিভক্ত করে, প্রতিটি খণ্ডকে মডেলের উত্সের চারপাশে কেন্দ্রীভূত করে এবং স্কেলিং করে এটিকে সমাধান করতে পারেন যাতে প্রতিটি খণ্ডের সমস্ত শীর্ষবিন্দু [-1, 1] পরিসরের মধ্যে ফিট হয়, যাতে ভাসমান বিন্দুর জন্য সর্বোচ্চ নির্ভুলতা রয়েছে। মান কম্প্রেশন জন্য pseudocode এই মত দেখায়:
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
vec3<float16> result = vec3(f32_to_f16(p.x), f32_to_f16(p.y), f32_to_f16(p.z));
রেন্ডার করার সময় শীর্ষবিন্দু ডেটা ডিকম্প্রেস করার জন্য আপনি মডেল ম্যাট্রিক্সে স্কেল ফ্যাক্টর এবং অনুবাদ বেক করুন। মনে রাখবেন যে আপনি স্বাভাবিক পরিবর্তনের জন্য এই একই মডেল ম্যাট্রিক্স ব্যবহার করতে চান না, কারণ তাদের একই কম্প্রেশন প্রয়োগ করা হয়নি। নরমালের জন্য এই ডিকম্প্রেশন ট্রান্সফর্মেশন ছাড়াই আপনার একটি ম্যাট্রিক্সের প্রয়োজন হবে, অথবা আপনি বেস মডেল ম্যাট্রিক্স ব্যবহার করতে পারেন (যা আপনি নরমালের জন্য ব্যবহার করতে পারেন) এবং তারপর শেডারের মধ্যে মডেল ম্যাট্রিক্সে অতিরিক্ত ডিকম্প্রেশন ট্রান্সফর্মেশন প্রয়োগ করতে পারেন। একটি উদাহরণ:
vec3 in in_pos;
void main() {
...
// bounding box data packed into uniform buffer
vec3 decompress_pos = in_pos * half_size_bounding_box + center_of_bounding_box;
gl_Position = proj * view * model * decompress_pos;
}
আরেকটি পদ্ধতির মধ্যে স্বাক্ষরিত স্বাভাবিক পূর্ণসংখ্যা (SNORM) ব্যবহার করা জড়িত। SNORM ডেটা প্রকারগুলি [-1, 1]-এর মধ্যে মানগুলিকে উপস্থাপন করতে ভাসমান বিন্দুর পরিবর্তে পূর্ণসংখ্যা ব্যবহার করে। অবস্থানের জন্য একটি 16-বিট SNORM ব্যবহার করা আপনাকে অ-ইউনিফর্ম ডিস্ট্রিবিউশনের ত্রুটি ছাড়াই একটি ফ্লোট16 হিসাবে একই মেমরি সঞ্চয় দেয়। SNORM ব্যবহার করার জন্য আমরা সুপারিশকৃত একটি বাস্তবায়ন এইরকম দেখাচ্ছে:
const int BITS = 16
for each position p in Mesh:
p -= center_of_bounding_box // Moves Mesh back to the center of model space
p /= half_size_bounding_box // Fits the mesh into a [-1, 1] cube
// float to integer value conversion
p = clamp(p * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
| বিন্যাস | আকার | |
|---|---|---|
| আগে | vec4< float32 > | 16 বাইট |
| পরে | vec3< float16/SNORM16 > | 6 বাইট |
ভার্টেক্স স্বাভাবিক এবং স্পর্শক স্থান
আলোর জন্য ভার্টেক্স সাধারন প্রয়োজন, এবং স্বাভাবিক ম্যাপিং এর মত আরও জটিল কৌশলগুলির জন্য স্পর্শক স্থান প্রয়োজন।
স্পর্শক স্থান
স্পর্শক স্থান হল একটি স্থানাঙ্ক ব্যবস্থা যেখানে প্রতিটি শীর্ষবিন্দুতে স্বাভাবিক, স্পর্শক এবং বিট্যানজেন্ট ভেক্টর থাকে। যেহেতু এই তিনটি ভেক্টর সাধারণত একে অপরের সাথে অর্থোগোনাল হয়, তাই আমাদের শুধুমাত্র তাদের দুটিকে সংরক্ষণ করতে হবে এবং ভার্টেক্স শেডারে অন্য দুটির ক্রস পণ্য নিয়ে তৃতীয়টি গণনা করতে পারি।
এই ভেক্টরগুলিকে সাধারণত 16-বিট ফ্লোট ব্যবহার করে উপস্থাপন করা যেতে পারে ভিজ্যুয়াল ফিডেলিটিতে কোনো ইন্দ্রিয়গত ক্ষতি ছাড়াই, তাই এটি শুরু করার জন্য একটি ভাল জায়গা!
আমরা QTangents নামে পরিচিত একটি কৌশলের সাহায্যে আরও সংকুচিত করতে পারি যা একটি একক চতুর্ভুজে সমগ্র স্পর্শক স্থান সংরক্ষণ করে। যেহেতু quaternions ঘূর্ণন প্রতিনিধিত্ব করতে ব্যবহার করা যেতে পারে, একটি ঘূর্ণন প্রতিনিধিত্বকারী 3x3 ম্যাট্রিক্সের কলাম ভেক্টর হিসাবে স্পর্শক স্থান ভেক্টর হিসাবে চিন্তা করে (এই ক্ষেত্রে মডেল স্পেস থেকে স্পর্শক স্থানে) আমরা দুটির মধ্যে রূপান্তর করতে পারি! একটি কোয়াটারনিয়নকে vec4 ডেটা-ভিত্তিক হিসাবে বিবেচনা করা যেতে পারে, এবং উপরে লিঙ্ক করা কাগজের উপর ভিত্তি করে ট্যানজেন্ট স্পেস ভেক্টর থেকে QTangent-এ রূপান্তর এবং এখানে বাস্তবায়ন থেকে অভিযোজিত হয়েছে:
const int BITS = 16
quaternion tangent_space_to_quat(vec3 normal, vec3 tangent, vec3 bitangent) {
mat3 tbn = {normal, tangent, bitangent};
quaternion qTangent(tbn);
qTangent.normalize();
//Make sure QTangent is always positive
if (qTangent.w < 0)
qTangent = -qTangent;
const float bias = 1.0 / (2^(BITS - 1) - 1);
//Because '-0' sign information is lost when using integers,
//we need to apply a "bias"; while making sure the Quaternion
//stays normalized.
// ** Also our shaders assume qTangent.w is never 0. **
if (qTangent.w < bias) {
Real normFactor = Math::Sqrt( 1 - bias * bias );
qTangent.w = bias;
qTangent.x *= normFactor;
qTangent.y *= normFactor;
qTangent.z *= normFactor;
}
//If it's reflected, then make sure .w is negative.
vec3 naturalBinormal = cross_product(tangent, normal);
if (dot_product(naturalBinormal, binormal) <= 0)
qTangent = -qTangent;
return qTangent;
}
quaternion স্বাভাবিক করা হবে, এবং আপনি SNORM ব্যবহার করে এটি সংকুচিত করতে সক্ষম হবেন। 16-বিট SNORM ভাল নির্ভুলতা এবং মেমরি সঞ্চয় দেয়। 8-বিট এসএনওআরএমগুলি আরও বেশি সঞ্চয় প্রদান করতে পারে, তবে অত্যন্ত স্পেকুলার উপকরণগুলিতে শিল্পকর্মের কারণ হতে পারে। আপনি উভয়ই চেষ্টা করে দেখতে পারেন এবং আপনার সম্পদের জন্য কোনটি সেরা কাজ করে তা দেখতে পারেন! quaternion এনকোডিং এই মত দেখায়:
for each vertex v in mesh:
quaternion res = tangent_space_to_quat(v.normal, v.tangent, v.bitangent);
// Once we have the quaternion we can compress it
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1);
ভার্টেক্স শেডারে কোয়াটারনিয়ন ডিকোড করতে ( এখান থেকে অভিযোজিত ):
vec3 xAxis( vec4 qQuat )
{
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwy = fTy * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxy = fTy * qQuat.x;
float fTxz = fTz * qQuat.x;
float fTyy = fTy * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( 1.0-(fTyy+fTzz), fTxy+fTwz, fTxz-fTwy );
}
vec3 yAxis( vec4 qQuat )
{
float fTx = 2.0 * qQuat.x;
float fTy = 2.0 * qQuat.y;
float fTz = 2.0 * qQuat.z;
float fTwx = fTx * qQuat.w;
float fTwz = fTz * qQuat.w;
float fTxx = fTx * qQuat.x;
float fTxy = fTy * qQuat.x;
float fTyz = fTz * qQuat.y;
float fTzz = fTz * qQuat.z;
return vec3( fTxy-fTwz, 1.0-(fTxx+fTzz), fTyz+fTwx );
}
void main() {
vec4 qtangent = normalize(in_qtangent); //Needed because 16-bit quantization
vec3 normal = xAxis(qtangent);
vec3 tangent = yAxis(qtangent);
float biNormalReflection = sign(in_qtangent.w); //ensured qtangent.w != 0
vec3 binormal = cross(normal, tangent) * biNormalReflection;
...
}
| বিন্যাস | আকার | |
|---|---|---|
| আগে | vec3< float32 > + vec3< float32 > + vec3< float32 > | 36 বাইট |
| পরে | vec4< SNORM16 > | 8 বাইট |
শুধুমাত্র স্বাভাবিক
যদি আপনার শুধুমাত্র স্বাভাবিক ভেক্টর সঞ্চয় করতে হয়, তবে একটি ভিন্ন পদ্ধতি রয়েছে যা আরও সঞ্চয়ের দিকে পরিচালিত করতে পারে - সাধারণ ভেক্টরকে সংকুচিত করতে কার্টেসিয়ান স্থানাঙ্কের পরিবর্তে ইউনিট ভেক্টরের অক্টেহেড্রাল ম্যাপিং ব্যবহার করে। অক্টাহেড্রাল ম্যাপিং একটি একক গোলককে একটি অষ্টহেড্রনে প্রজেক্ট করে এবং তারপর অষ্টহেড্রনটিকে একটি 2D সমতলে প্রজেক্ট করে কাজ করে। ফলাফল হল যে আপনি মাত্র দুটি সংখ্যা ব্যবহার করে যেকোনো সাধারণ ভেক্টরকে উপস্থাপন করতে পারেন। এই দুটি সংখ্যাকে আমরা টেক্সচার কোঅর্ডিনেট হিসাবে ভাবা যেতে পারে যে 2D সমতলকে আমরা "নমুনা" করতে ব্যবহার করি আমরা গোলকটিকে সম্মুখে প্রজেক্ট করেছি, যা আমাদের মূল ভেক্টর পুনরুদ্ধার করতে দেয়। এই দুটি সংখ্যা তারপর একটি SNORM8 সংরক্ষণ করা যেতে পারে.
চিত্র 2: অক্টেহেড্রাল ম্যাপিং ভিজ্যুয়ালাইজড ( উৎস )
const int BITS = 8
// Assumes the vector is unit length
// sign() function should return positive for 0
for each normal n in mesh:
float invL1Norm = 1.0 / (abs(n.x) + abs(n.y) + abs(n.z));
vec2 res;
if (n.z < 0.0) {
res.x = (1.0 - abs(n.y * invL1Norm)) * sign(n.x);
res.y = (1.0 - abs(n.x * invL1Norm)) * sign(n.y);
} else {
res.x = n.x * invL1Norm;
res.y = n.y * invL1Norm;
}
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
ভার্টেক্স শেডারে ডিকম্প্রেশন (আবার কার্টেসিয়ান স্থানাঙ্কে রূপান্তর করতে) সস্তা; বেশিরভাগ আধুনিক মোবাইল ডিভাইসের সাথে আমরা এই কৌশলটি বাস্তবায়ন করার সময় কোন বড় কর্মক্ষমতা অবনতি দেখতে পাইনি। ভার্টেক্স শেডারে ডিকম্প্রেশন:
//Additional Optimization: twitter.com/Stubbesaurus/status/937994790553227264
vec3 oct_to_vec(vec2 e):
vec3 v = vec3(e.xy, 1.0 - abs(e.x) - abs(e.y));
float t = max(-v.z, 0.0);
v.xy += t * -sign(v.xy);
return v;
এই পদ্ধতিটি সম্পূর্ণ স্পর্শক স্থান সংরক্ষণ করতেও ব্যবহার করা যেতে পারে, এই কৌশলটি ব্যবহার করে vec2< SNORM8 > ব্যবহার করে স্বাভাবিক এবং স্পর্শক ভেক্টর সংরক্ষণ করার জন্য তবে আপনাকে বিট্যানজেন্টের দিক সংরক্ষণ করার জন্য একটি উপায় খুঁজে বের করতে হবে (সাধারণ দৃশ্যের জন্য প্রয়োজন যেখানে আপনি একটি মডেলে UV স্থানাঙ্ক মিরর করেছেন)। এটি বাস্তবায়নের একটি উপায় হল আপনার স্পর্শক ভেক্টর এনকোডিংয়ের একটি উপাদানকে সর্বদা ইতিবাচক হওয়ার জন্য ম্যাপ করা, তারপর আপনি যদি বিট্যাঞ্জেন্ট দিকটি ফ্লিপ করতে চান তবে এটির চিহ্নটি ফ্লিপ করুন এবং ভার্টেক্স শেডারে এটি পরীক্ষা করুন:
const int BITS = 8
const float bias = 1.0 / (2^(BITS - 1) - 1)
// Compressing
for each normal n in mesh:
//encode to octahedron, result in range [-1, 1]
vec2 res = vec_to_oct(n);
// map y to always be positive
res.y = res.y * 0.5 + 0.5;
// add a bias so that y is never 0 (sign in the vertex shader)
if (res.y < bias)
res.y = bias;
// Apply the sign of the binormal to y, which was computed elsewhere
if (binormal_sign < 0)
res.y *= -1;
res = clamp(res * (2^(BITS - 1) - 1), -2^(BITS - 1), 2^(BITS - 1) - 1)
// Vertex shader decompression
vec2 encode = vec2(tangent_encoded.x, abs(tangent_encoded.y) * 2.0 - 1.0));
vec3 tangent_real = oct_to_vec3(encode);
float binormal_sign = sign(tangent_encode.y);
| বিন্যাস | আকার | |
|---|---|---|
| আগে | vec3< float32 > | 12 বাইট |
| পরে | vec2< SNORM8 > | 2 বাইট |
ভার্টেক্স ইউভি স্থানাঙ্ক
ইউভি কোঅর্ডিনেট, টেক্সচার ম্যাপিংয়ের জন্য ব্যবহৃত (অন্যান্য জিনিসগুলির মধ্যে), সাধারণত 32 বিট ফ্লোট ব্যবহার করে সংরক্ষণ করা হয়। এগুলিকে 16 বিট ফ্লোট দিয়ে সংকুচিত করার ফলে 1024x1024 এর চেয়ে বড় টেক্সচারের জন্য নির্ভুলতা সমস্যা হয়; [0.5, 1.0] এর মধ্যে ফ্লোটিং-পয়েন্ট নির্ভুলতার মানে হল যে মানগুলি 1 পিক্সেলের চেয়ে বড় বৃদ্ধি পাবে!
উত্তম পন্থা হল স্বাক্ষরবিহীন স্বাভাবিক পূর্ণসংখ্যা (UNORM), বিশেষ করে UNORM16 ব্যবহার করা; এটি 65536x65536 পর্যন্ত টেক্সচার সমর্থন করে সমগ্র টেক্সচার সমন্বয় পরিসর জুড়ে অভিন্ন বন্টন প্রদান করে! এটি অনুমান করে যে টেক্সচার স্থানাঙ্কগুলি প্রতি উপাদানের [0.0, 1.0] সীমার মধ্যে রয়েছে, যা জালের উপর নির্ভর করে এমন নাও হতে পারে (উদাহরণস্বরূপ, দেয়ালগুলি 1.0 এর বাইরে যায় এমন টেক্সচার স্থানাঙ্ক ব্যবহার করতে পারে) তাই এই কৌশলটি দেখার সময় মনে রাখবেন . রূপান্তর ফাংশন এই মত দেখাবে:
const int BITS = 16
for each vertex_uv V in mesh:
V *= clamp(2^BITS - 1, 0, 2^BITS - 1); // float to integer value conversion
| বিন্যাস | আকার | |
|---|---|---|
| আগে | vec2< float32 > | 8 বাইট |
| পরে | vec2< UNORM16 > | 4 বাইট |
ভার্টেক্স কম্প্রেশন ফলাফল
এই ভার্টেক্স কম্প্রেশন কৌশলগুলি ভার্টেক্স মেমরি স্টোরেজের 66% হ্রাসের দিকে পরিচালিত করে, যা 48 বাইট থেকে 16 বাইটে নেমে যায়। এটি নিজেকে প্রকাশ করেছে:
- ভার্টেক্স মেমরি রিড ব্যান্ডউইথ:
- বিনিং: 27GB/s থেকে 9GB/s
- রেন্ডারিং: 4.5B/s থেকে 1.5GB/s
- ভার্টেক্স ফেচ স্টল:
- বিনিং: 50% থেকে 0%
- রেন্ডারিং: 90% থেকে 90%
- গড় বাইট/ভারটেক্স:
- বিনিং: 48B থেকে 16B
- রেন্ডারিং: 52B থেকে 18B
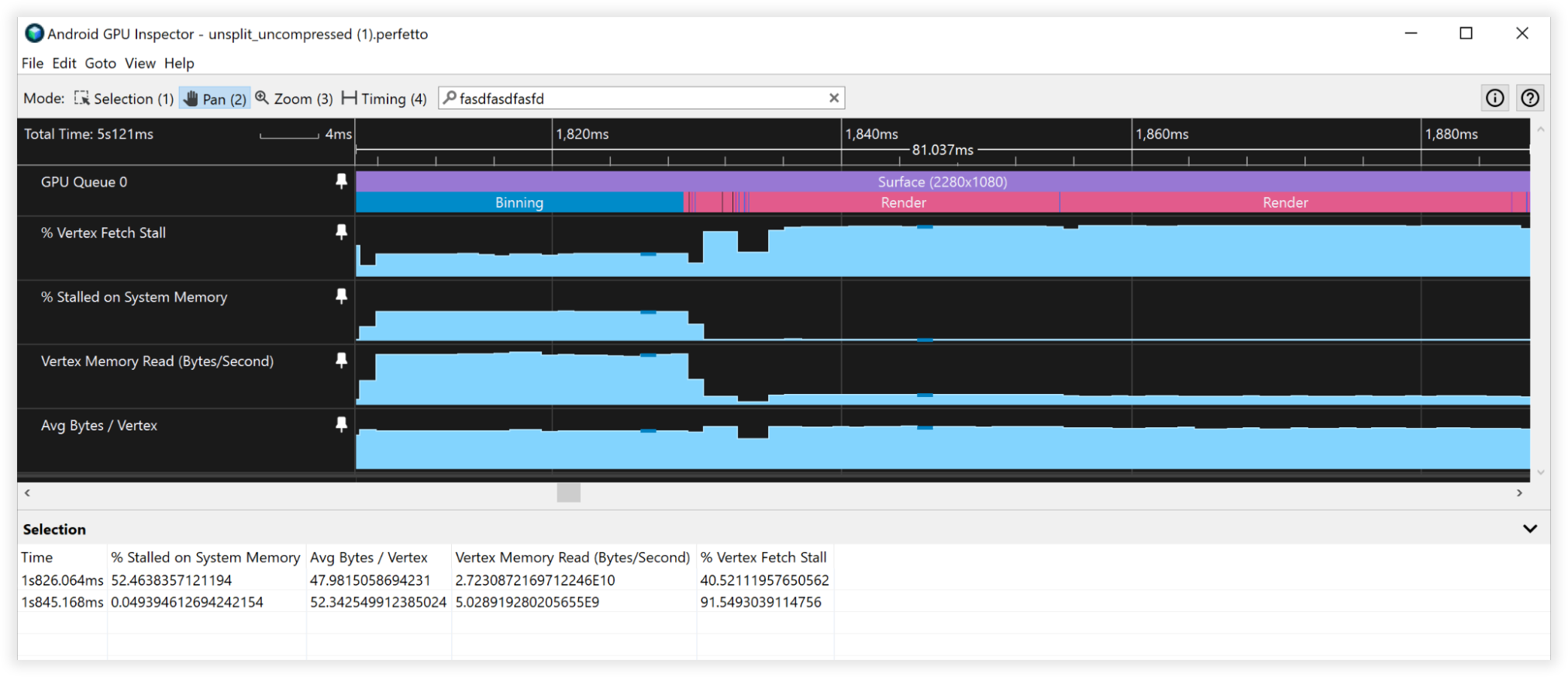
চিত্র 3: কম্প্রেসড শীর্ষবিন্দুগুলির Android GPU পরিদর্শক দৃশ্য
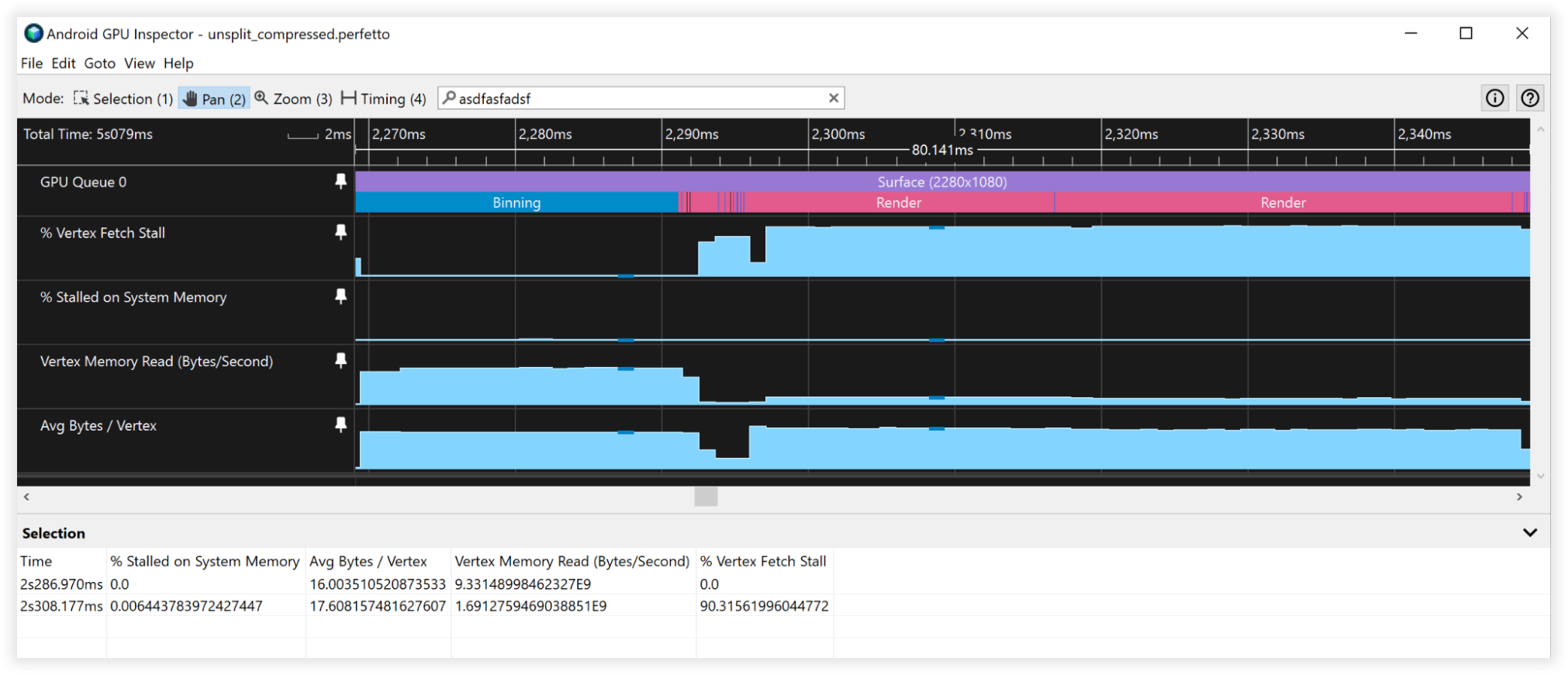
চিত্র 4: সংকুচিত শীর্ষবিন্দুগুলির Android GPU পরিদর্শক দৃশ্য
ভার্টেক্স স্ট্রীম স্প্লিটিং
ভার্টেক্স স্ট্রীম স্প্লিটিং ভার্টেক্স বাফারে ডেটার সংগঠনকে অপ্টিমাইজ করে। এটি একটি ক্যাশে পারফরম্যান্স অপ্টিমাইজেশান যা সাধারণত অ্যান্ড্রয়েড ডিভাইসগুলিতে পাওয়া টাইল-ভিত্তিক জিপিইউগুলিতে একটি পার্থক্য তৈরি করে - বিশেষ করে রেন্ডারিং প্রক্রিয়ার বাইনিং ধাপে।
টাইল-ভিত্তিক GPU গুলি একটি শেডার তৈরি করে যা বিনিং করার জন্য প্রদত্ত ভার্টেক্স শেডারের উপর ভিত্তি করে স্বাভাবিক ডিভাইস স্থানাঙ্ক গণনা করে। দৃশ্যমান হোক বা না হোক, দৃশ্যের প্রতিটি শীর্ষে প্রথমে এটি কার্যকর করা হয়। ভার্টেক্স পজিশন ডেটা মেমরিতে সংলগ্ন রাখা তাই একটি বড় প্লাস। অন্যান্য জায়গায় এই ভার্টেক্স স্ট্রীম লেআউটটি শ্যাডো পাসের জন্য উপকারী হতে পারে, সাধারণত আপনার শুধুমাত্র ছায়া গণনার জন্য পজিশন ডেটার প্রয়োজন হয়, সেইসাথে গভীরতা প্রিপাস, যা সাধারণত কনসোল/ডেস্কটপ রেন্ডারিংয়ের জন্য ব্যবহৃত একটি কৌশল; এই ভার্টেক্স স্ট্রীম লেআউট রেন্ডারিং ইঞ্জিনের একাধিক ক্লাসের জন্য একটি জয় হতে পারে!
স্ট্রীম স্প্লিটিং-এর মধ্যে শীর্ষবিন্দুর অবস্থান ডেটার একটি সংলগ্ন অংশের সাথে শীর্ষবিন্দু বাফার সেট আপ করা এবং ইন্টারলিভড ভার্টেক্স বৈশিষ্ট্য সম্বলিত আরেকটি বিভাগ জড়িত। বেশিরভাগ অ্যাপ্লিকেশনগুলি সাধারণত তাদের বাফারগুলি সম্পূর্ণরূপে সমস্ত বৈশিষ্ট্যগুলিকে সংযুক্ত করে সেট আপ করে। এই চাক্ষুষ পার্থক্য ব্যাখ্যা করে:
Before:
|Position1/Normal1/Tangent1/UV1/Position2/Normal2/Tangent2/UV2......|
After:
|Position1/Position2...|Normal1/Tangent1/UV1/Normal2/Tangent2/UV2...|
GPU কীভাবে ভার্টেক্স ডেটা আনে তা আমাদের স্ট্রিম বিভাজনের সুবিধাগুলি বুঝতে সাহায্য করে। তর্কের খাতিরে ধরে নিচ্ছি:
- 32 বাইট ক্যাশে লাইন (একটি বেশ সাধারণ আকার)
- ভার্টেক্স বিন্যাস এর মধ্যে রয়েছে:
- অবস্থান, vec3<float32> = 12 বাইট
- সাধারণ vec3<float32> = 12 বাইট
- UV স্থানাঙ্ক vec2<float32> = 8 বাইট
- মোট আকার = 32 বাইট
যখন জিপিইউ বিনিংয়ের জন্য মেমরি থেকে ডেটা আনে, তখন এটি চালানোর জন্য একটি 32-বাইট ক্যাশে লাইন টানবে। ভার্টেক্স স্ট্রীম স্প্লিটিং ছাড়াই, এটি আসলে এই ক্যাশে লাইনের প্রথম 12 বাইটগুলিকে বিনিংয়ের জন্য ব্যবহার করবে এবং পরবর্তী 20 বাইটগুলিকে বাতিল করে দেবে কারণ এটি পরবর্তী ভার্টেক্স নিয়ে আসে৷ ভার্টেক্স স্ট্রীম স্প্লিটিংয়ের সাথে, শীর্ষস্থানীয় অবস্থানগুলি মেমরিতে সংলগ্ন থাকবে, তাই যখন সেই 32-বাইট খণ্ডটি ক্যাশে টেনে আনা হয়, তখন এটিতে আরও আনতে মূল মেমরিতে ফিরে যাওয়ার আগে কাজ করার জন্য 2টি সম্পূর্ণ শীর্ষস্থানীয় অবস্থান থাকবে, একটি 2x উন্নতি!
এখন, যদি আমরা ভার্টেক্স স্ট্রীম স্প্লিটিংকে ভার্টেক্স কম্প্রেশনের সাথে একত্রিত করি, তাহলে আমরা একটি একক ভার্টেক্স পজিশনের সাইজ কমিয়ে 6 বাইটে নামিয়ে ফেলব, তাই সিস্টেম মেমরি থেকে টেনে নেওয়া একটি একক 32-বাইট ক্যাশে লাইনে কাজ করার জন্য 5টি সম্পূর্ণ ভার্টেক্স পজিশন থাকবে, একটি 5x উন্নতি!
ভার্টেক্স স্ট্রীম বিভাজন ফলাফল
- ভার্টেক্স মেমরি রিড ব্যান্ডউইথ:
- বিনিং: 27GB/s থেকে 6.5GB/s
- রেন্ডারিং: 4.5GB/s থেকে 4.5GB/s
- ভার্টেক্স ফেচ স্টল:
- বিনিং: 40% থেকে 0%
- রেন্ডারিং: 90% থেকে 90%
- গড় বাইট/ভারটেক্স:
- বিনিং: 48B থেকে 12B
- রেন্ডারিং: 52B থেকে 52B

চিত্র 5: আনস্প্লিট ভার্টেক্স স্ট্রীমগুলির Android GPU ইন্সপেক্টর ভিউ
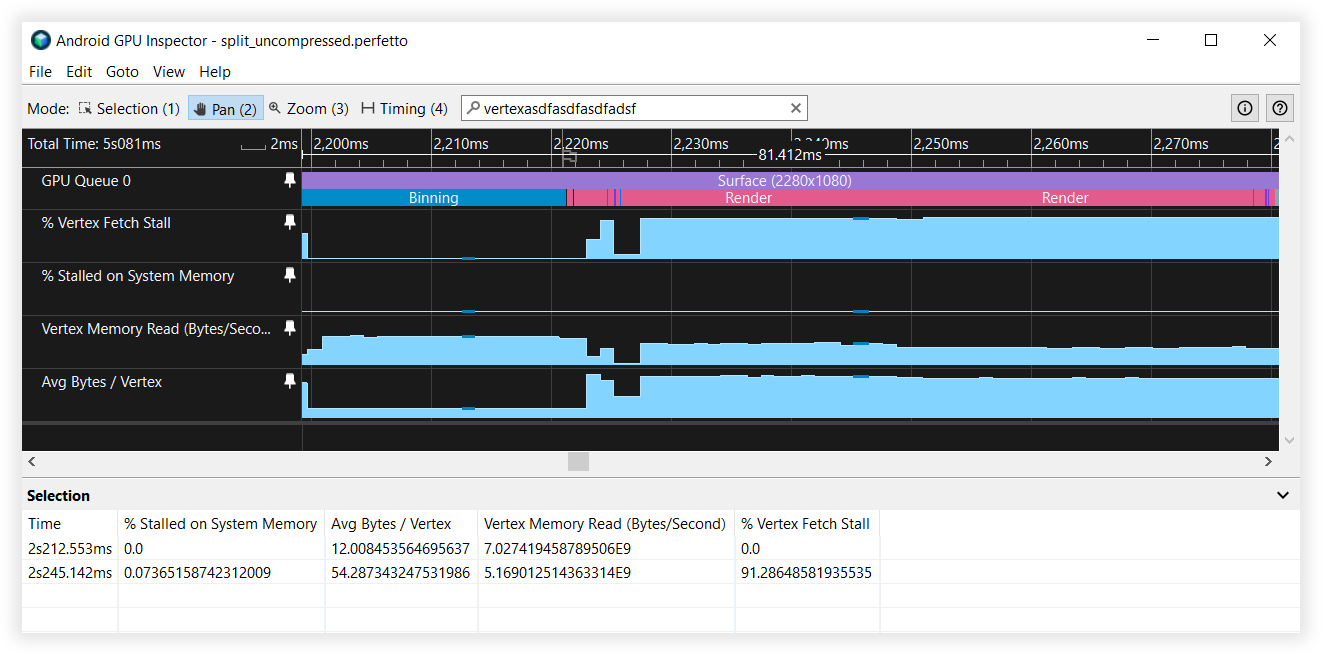
চিত্র 6: স্প্লিট ভার্টেক্স স্ট্রীমগুলির অ্যান্ড্রয়েড জিপিইউ ইন্সপেক্টর ভিউ
যৌগিক ফলাফল
- ভার্টেক্স মেমরি রিড ব্যান্ডউইথ:
- বিনিং: 25GB/s থেকে 4.5GB/s
- রেন্ডারিং: 4.5GB/s থেকে 1.7GB/s
- ভার্টেক্স ফেচ স্টল:
- বিনিং: 41% থেকে 0%
- রেন্ডারিং: 90% থেকে 90%
- গড় বাইট/ভারটেক্স:
- বিনিং: 48B থেকে 8B
- রেন্ডারিং: 52B থেকে 19B

চিত্র 7: আনসপ্লিট, আনকম্প্রেসড ভার্টেক্স স্ট্রীমগুলির অ্যান্ড্রয়েড জিপিইউ ইন্সপেক্টর ভিউ
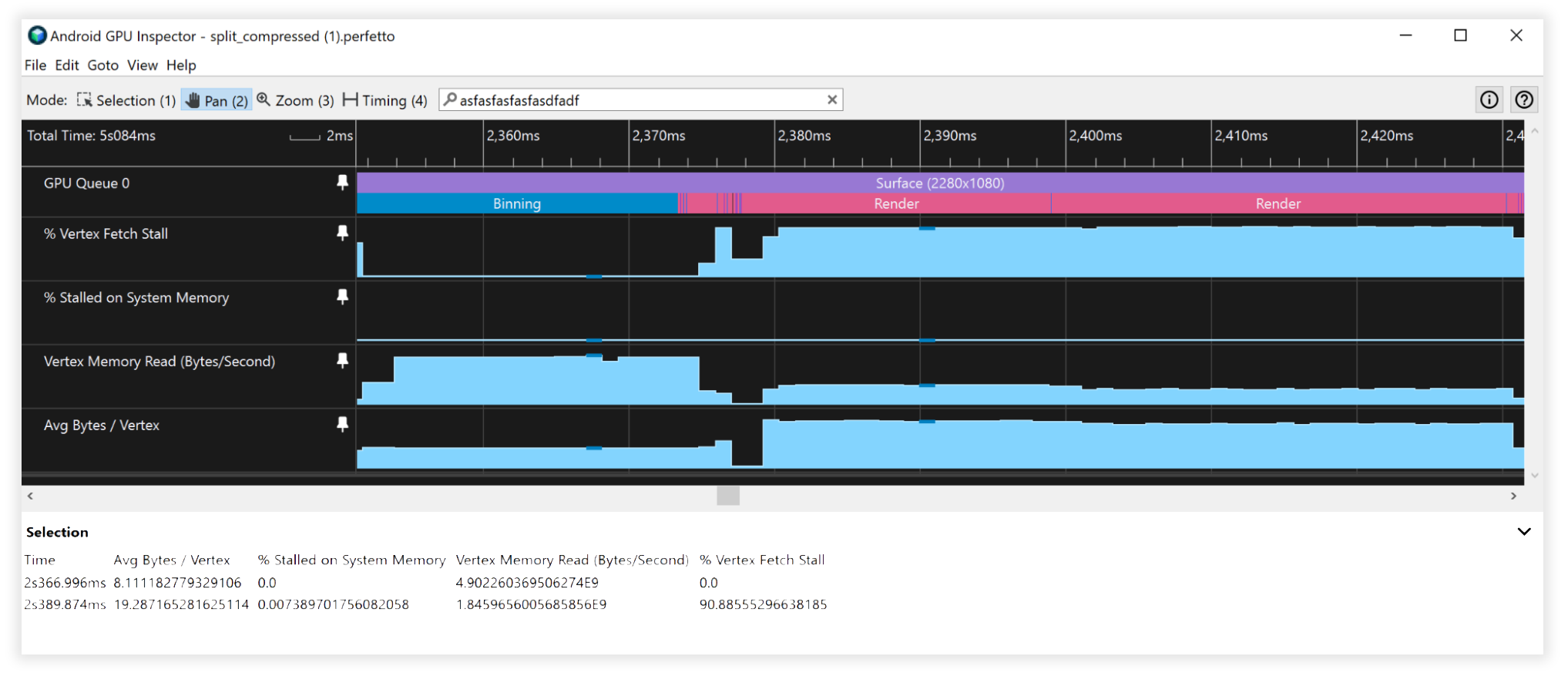
চিত্র 8: অ্যান্ড্রয়েড জিপিইউ পরিদর্শক বিভক্ত, সংকুচিত শীর্ষবিন্দু স্ট্রীম
অতিরিক্ত বিবেচনা
16 বনাম 32 বিট ইনডেক্স বাফার ডেটা
- সর্বদা বিভক্ত/খণ্ড মেশগুলি যাতে তারা একটি 16-বিট সূচক বাফারে ফিট করে (সর্বোচ্চ 65536 অনন্য শীর্ষ)। এটি মোবাইলে ইনডেক্স রেন্ডারিংয়ে সহায়তা করবে কারণ এটি ভার্টেক্স ডেটা আনার জন্য সস্তা এবং কম শক্তি খরচ করবে৷
অসমর্থিত ভার্টেক্স বাফার অ্যাট্রিবিউট ফরম্যাট
- SSCALED ভার্টেক্স ফর্ম্যাটগুলি মোবাইলে ব্যাপকভাবে সমর্থিত নয়, এবং যখন ব্যবহার করা হয় তখন ড্রাইভারগুলিতে ব্যয়বহুল পারফরম্যান্স ট্রেড-অফ হতে পারে যা তাদের হার্ডওয়্যার সমর্থন না থাকলে তাদের অনুকরণ করার চেষ্টা করে। সর্বদা SNORM-এর জন্য যান এবং ডিকম্প্রেস করার জন্য নগণ্য ALU খরচ প্রদান করুন।


